Harrell's little crib sheet on series -
examples
© Copyright 2000 by Evans M. Harrell II
- (geometric series) Suppose you are paying off a college loan with
initial
value p0, interest rate per period r, and payment m.
At the end of payment period n, the amount
you owe is pn = pn-1 (1+r) - m.
Use the geometric series to solve for pn in terms of
p0, r, and m. When is the loan paid off?
- (p-series) Put a unit mass on every integer point of the positive
x-axis. Will the gravitational force on a particle, such as yourself,
standing at the origin be finite or infinite? (Gravity is an
inverse-square force.) Variants: a) Put mass sin2(n) at
x=n; b)
Put mass n at x=n; c)
Put mass n1/2 at x=n.
-
Use your knowledge of the derivative of the arctan(x) to find its
Taylor series painlessly. Use the result to evaluate the series

- (convergence by Taylor) Use the ratio test to verify that
 converges. Then
use Taylor series and some ingenuity to find the limit.
converges. Then
use Taylor series and some ingenuity to find the limit.
- (hitting with calculus) Integrate the geometric series
in x term by term to get another Taylor series. To what function
does it converge? For what x does it converge?
- (bigger than an elephant)
 diverges, because
diverges, because  at least for n > 2, and
the first million terms don't matter. So this series is bigger than
half an arithmetic series, which diverges.
at least for n > 2, and
the first million terms don't matter. So this series is bigger than
half an arithmetic series, which diverges.
- (lack of commitment) The series
 can't make up his mind whether to settle down with with 0 or 1.
The more adventuresome students can think about
can't make up his mind whether to settle down with with 0 or 1.
The more adventuresome students can think about

- (ratio with
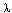 > 1) Explain why the ratio test for divergent series is
equivalent to the comparison test with a diverging geometric
series.
> 1) Explain why the ratio test for divergent series is
equivalent to the comparison test with a diverging geometric
series.
- (smaller than a bug)
Use comparison to show that
 converges.
Could any other convergence tests also squash this series?
converges.
Could any other convergence tests also squash this series?
- (ratio test) Explain why the ratio test for convergent series is
equivalent to the comparison test with a converging geometric
series.
- (ratio test) Tip: This is a good test to apply if there are terms
like n! and cn in an
(examples).
- (alternating series) Consider the alternating sum of the
reciprocals of the odd integers,
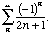 . Use your calculator to get
an impression of how rapidly it converges. Use the
Taylor series for the arctangent
, above,
to find its sum. Discuss what happens if it is summed
in other orders.
. Use your calculator to get
an impression of how rapidly it converges. Use the
Taylor series for the arctangent
, above,
to find its sum. Discuss what happens if it is summed
in other orders.
Return to
crib sheet

 converges. Then
use Taylor series and some ingenuity to find the limit.
converges. Then
use Taylor series and some ingenuity to find the limit.
 diverges, because
diverges, because  at least for n > 2, and
the first million terms don't matter. So this series is bigger than
half an arithmetic series, which diverges.
at least for n > 2, and
the first million terms don't matter. So this series is bigger than
half an arithmetic series, which diverges.
 can't make up his mind whether to settle down with with 0 or 1.
The more adventuresome students can think about
can't make up his mind whether to settle down with with 0 or 1.
The more adventuresome students can think about

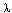 > 1) Explain why the ratio test for divergent series is
equivalent to the comparison test with a diverging geometric
series.
> 1) Explain why the ratio test for divergent series is
equivalent to the comparison test with a diverging geometric
series.
 converges.
Could any other convergence tests also squash this series?
converges.
Could any other convergence tests also squash this series?
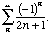 . Use your calculator to get
an impression of how rapidly it converges. Use the
Taylor series for the arctangent
, above,
to find its sum. Discuss what happens if it is summed
in other orders.
. Use your calculator to get
an impression of how rapidly it converges. Use the
Taylor series for the arctangent
, above,
to find its sum. Discuss what happens if it is summed
in other orders.