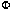 is a continuous, linear function from E to R (or the complex numbers C),
and
is a continuous, linear function from E to R (or the complex numbers C),
and
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
(a)
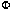 is a continuous, linear function from E to R (or the complex numbers C),
and
is a continuous, linear function from E to R (or the complex numbers C),
and
(b) there is a unique member v of E such that
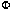 (x) = < x, v >
; for
each x in E.
(x) = < x, v >
; for
each x in E.
First, let us formalize the
Projection lemma.
Let H be a Hilbert space and M a closed subspace. Let Mperp consist of the vectors which are orthogonal to all the vectors of M. Given any vector x in H, there is a unique vector y in M and a unique z in Mperp such that x = y + z. The function associating y to x is a linear projection operator, as is the function associating z to x.
The Riesz lemma, stated in words, claims that
every continuous linear functional
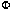 comes from an inner product.
comes from an inner product.
Proof of the Riesz lemma:
Consider the null space
N = N(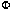 ), which is a closed subspace.
If N = H, then
), which is a closed subspace.
If N = H, then
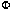 is just the zero function, and g = 0.
This is the trivial case. Otherwise, There must be a nonzero vector in
Nperp. In fact, Nperp is one-dimensional, since if there were two linearly independent vectors
z1,2 in Nperp, then we can choose numbers
a and b, different from 0, such that
is just the zero function, and g = 0.
This is the trivial case. Otherwise, There must be a nonzero vector in
Nperp. In fact, Nperp is one-dimensional, since if there were two linearly independent vectors
z1,2 in Nperp, then we can choose numbers
a and b, different from 0, such that
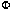 (a z1-b z2) =
a
(a z1-b z2) =
a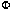 (z1)
- b
(z1)
- b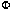 (z2) = 0.
(z2) = 0.
Now scale z1 so that 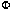 (z1) is a real number and then let
(z1) is a real number and then let
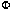 (z1) z1/||z1||.
(z1) z1/||z1||.
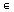 N. Notice also that
N. Notice also that
We calculate:
 (x) = a
(x) = a  (g) + 0
= < a g + (x-a g), g> = < x, g>
(g) + 0
= < a g + (x-a g), g> = < x, g>
QED