Linear Methods of Applied Mathematics

Evans M. Harrell II and James V. Herod*

*(c) Copyright 1996, 2010 by Evans M. Harrell II and James V. Herod. All rights reserved.

1.

a) Solve the following problem:

   PDE u_t = 4 u_xx, for 0 < t, 0 < x < 1

   BC u_x(t,0) = 0, u_x(t,1) = 0, for 0 < t

   IC u(0,x) = 2 x - x², for 0 < x < 1

ANSWER:

u(t,x) = 2/3 - 4 Sum exp(-4 n²² t) cos(n x)/(n^{2 2}).

The way to get this solution is to recall that the separated solutions with these BC are either constants or of the form constant exp(-4 n^{2 2} t) cos(n x)/(n². The general solution is a sum of these solutions, with coefficients we could call a_n. When we put t = 0, we get a Fourier cosine series, and the coefficients are the Fourier cosine coefficients for 2 x - x². Then use the standard formula for these coefficients.

b) Find the maximum value of u(t,x) for 0 <= t <= 1, 0 <= x <= 1:

We know by the maximum principle that the maximum value occurs either at t=0, t = 1, x = 0, or x = 1, so only these values need to be considered. Physical reasoning can be used, if you wish, to eliminate all possibilities for t > 0 (the rod is insulated and has no sources, so heat cannot appear at the ends while the temperature relaxes to equilibrium). Considering t=0, we find:

ANSWER:

The maximum temperature occurs at x = 1, t = 0

The maximum temperature is u_max = 1

There is a complete, orthonormal set of functions denoted _n(x), for -infinity < x < infinity, which are eigenfunctions for the ordinary differential equation

- _n'' + x² _n = (2n+1) _n, n = 0, 1, 2, ....

You may use the notation _n in the answer to this problem.

Consider the following PDE:

    PDE u_tt = grad² u - x² u, for 0 < t, 0 < x < 1, 0 < y <

BC u(t,x,0) = u(t,x, ) = 0, for 0 < t

Find the normal mode with the lowest frequency of vibration (include the time dependence):

ANSWER:

This is a straightforward separation of variables, albeit with a new function. The function Y satisfies the usual eigenvalue equation with 0 Dirichlet BC, so the spatial part of the separated solutions are of the form _n sin(m y), n = 0, 1, ...; m = 1, 2, .... If the full solution is of the form T_nm(t) _n(x) sin(m y), then substituting into the PDE shows that

T_nm''(t) = 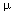_nm T_nm(t),

where 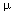_nm = (2 n + 1) + m². The solutions are sines and cosines of 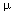_nm^1/2. The lowest frequency occurs when m = 0, n = 1:

u(t,x,y) = (A₀₁ cos(2^1/2 t) + B₀₁ sin(2^1/2 t) ) ₀(x) sin(y),

or, if you prefer,

u(t,x,y) = (A₀₁ cos(2^1/2 t) + B₀₁ sin(2^1/2 t) ) exp(-x²/2) sin(y).

Find the general solution:

ANSWER:

u(t,x,y) = Sum of (A_nm cos((2n+1+m²)^1/2 t) + B_nm sin((2n+1+m²)^1/2 t) ) _n(x) sin(m y), for n = 0, 1, ...; m = 1, 2, ....

0 < r < 20 cm,

0 < < /3 radians

0 < z < 1 cm.

It has come to thermal equilibrium while sitting on a student's computer monitor, so that the temperature on its surface is

u(r, , 0) = 30

u(r, , 1) = 20

u(r,0,z) = u(r, /3,z) = 30 - 10 z

u(20, ,z) = 30 - 10 z - 5

This is a low quality pizza consisting of a homogeneous material (independent of position)

a) The partial differential equation for a homogeneous material at thermal equilibrium is Laplace's equation,

    grad² u = 0

b) Answer the following questions.

Are there useful simplifications involving the boundary conditions? If so, what are they?

Be specific and put the answer here: Most of the boundary conditions can be made homogeneous by redefining the unknown as

    v(t,x) = u - (30 - 10 z).

The only BC which remains nonhomogeneous is the one at r = 20.

Are there useful separated solutions? If so, write the specific ordinary differential equations that the separated solutions satisfy below. Include boundary conditions.

write v(r,, z) = R(r) Q() Z(z). Then:

    - Q'' = 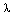Q,
    (0) = (/3) = 0

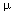    - Z'' = Z,
    Z(0) = Z(1) = 0

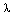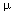    R'' + (1/r) R' = (/r² + ) R,
    R(0) bounded

(We don't do anything about the nonhomogeneous boundary before putting the separated solutions together.)

c) Solve the differential equations with the given boundary conditions.

The equation for R is our old friend Bessel's equation, but the eigenvalues 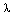are now determined by the conditions on Q, which lead to eigenfunctions of the form sin(3 m ) and eigenvalues 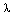_m = 9 m².

Back to the test.

Back to Chapter X

Return to Table of Contents

Return to Evans Harrell's home page