*©
Copyright 1994-2000 by Evans M. Harrell
II and James V. Herod. All rights reserved.
This document collects some standard vector identities
and relationships among coordinate systems in three dimensions. It is assumed
that all vector fields are differentiable arbitrarily often; if the vector
field is not sufficiently smooth, some of these formulae are in doubt.
Basic formulae
-
The dot product

quantifies the correlation between the vectors a and b .
-
The cross product

is the area of the parallelogram spanned by the vectors a and b.
Notice that
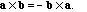
Unlike the dot product, which works in all dimensions, the cross product is
special to three dimensions.
-
The triple product
 has the value of the determinant of the matrix consisting of a,
b, and c as row vectors. It is unchanged by cyclic permutation:
has the value of the determinant of the matrix consisting of a,
b, and c as row vectors. It is unchanged by cyclic permutation:

Although the cross product is strictly three-dimensional, the generalization
of the triple product as a determinant is useful in all dimensions.
-
Other multiple products.
-
The gradient is defined on a scalar field f and produces a vector field,
denoted

It quantifies the rate of change and points in the direction of greatest
change.
-
The divergence is defined on a vector field v and produces a scalar
field, denoted

It quantifies the tendency of neighboring vectors to point away from one
another (or towards one another, if negative)
-
The curl is defined on a vector field and produces another vector field,
except that the curl of a vector field is not affected by reflection in the
same way as the vector field is. It is denoted
 Unlike the gradient and the divergence, which work in all dimensions, the curl
is special to three dimensions.
Unlike the gradient and the divergence, which work in all dimensions, the curl
is special to three dimensions.
-
The Laplacian is defined as
-
Product rules:
 or, equivalently, grad (f g) = f grad g + g grad f
or, equivalently, grad (f g) = f grad g + g grad f
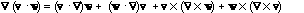
 or, equivalently, div(f v) = f div v + grad f . v
or, equivalently, div(f v) = f div v + grad f . v
 or, equivalently, curl(f v) = f curl v + grad f X v
or, equivalently, curl(f v) = f curl v + grad f X v
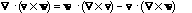
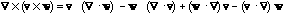
-
Chain rules
 or, equivalently, grad f(g(x)) = f'(g(x)) grad g(x)
or, equivalently, grad f(g(x)) = f'(g(x)) grad g(x)
 or, equivalently, df(w(t))/dt = grad f(w(t)) w'(t)
or, equivalently, df(w(t))/dt = grad f(w(t)) w'(t)
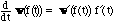
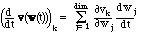
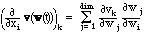
-
Integral identities (
Green's,
Gauss's,
and
Stokes's
identities):
Green's identities:
-
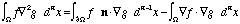
-
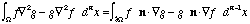
Gauss's divergence theorem:
-
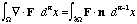
Stokes's theorem:
-
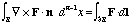
-
Relationships among the common three-dimensional coordinate systems.
-
Cartesian in spherical

-
Cartesian in cylindrical

- spherical in Cartesian

-
spherical in cylindrical

-
cylindrical in Cartesian
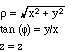
-
cylindrical in spherical

-
Cylindrical vector calculus. Let ek denote the unit vector in the
direction of increase of coordinate k. Then
-
Spherical vector calculus. Let ek denote the unit vector in the
direction of increase of coordinate k. Then
Return to Table of Contents
Return to Evans Harrell's home page