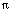 ) =
y''(
) =
y''(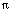 ) = 0.
) = 0.
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 24 March 2000
The following problem is best done with software because of some heavy algebra,
particularly for part (b).
Find two Green functions for the ordinary differential equation
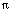 ) =
y''(
) =
y''(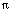 ) = 0.
) = 0.
Solution (parts a and b).
Solve[{b3 (Sinh[1]-Sin[1]) + b4 (Cosh[1]-Cos[1]) == -(1/2) (Sinh[1-t] - Sin[1-t]), \
b3 (Cosh[1]-Cos[1]) + b4 (Sinh[1]+Sin[1]) == -(1/2) (Cosh[1-t] - Cos[1-t])}, {b3,b4}]
-(-Sin[1 - t] + Sinh[1 - t])
{{b3 -> ---------------------------- +
2 (-Sin[1] + Sinh[1])
((-Cos[1] + Cosh[1]) (2 (-Cos[1 - t] + Cosh[1 - t]) (-Sin[1] + Sinh[1]) -
2 (-Cos[1] + Cosh[1]) (-Sin[1 - t] + Sinh[1 - t]))) /
2
((-Sin[1] + Sinh[1]) (-4 (-Cos[1] + Cosh[1]) + 4 (-Sin[1] + Sinh[1]) (Sin[1] + Sinh[1])))\
, b4 -> -((2 (-Cos[1 - t] + Cosh[1 - t]) (-Sin[1] + Sinh[1]) -
2 (-Cos[1] + Cosh[1]) (-Sin[1 - t] + Sinh[1 - t])) /
2
(-4 (-Cos[1] + Cosh[1]) + 4 (-Sin[1] + Sinh[1]) (Sin[1] + Sinh[1])))}}
Hence the Green function is:
G[x_,t_] = H[x-t] (Sinh[x-t] - Sin[x-t])/2 + \
b3 (Sinh[x] - Sin[x]) + b4 (Cosh[x] - Cos[x]) /. %
{-(((-Cos[x] + Cosh[x]) (2 (-Cos[1 - t] + Cosh[1 - t]) (-Sin[1] + Sinh[1]) -
2 (-Cos[1] + Cosh[1]) (-Sin[1 - t] + Sinh[1 - t]))) /
2
(-4 (-Cos[1] + Cosh[1]) + 4 (-Sin[1] + Sinh[1]) (Sin[1] + Sinh[1]))) +
H[-t + x] (Sin[t - x] - Sinh[t - x])
------------------------------------ +
2
-(-Sin[1 - t] + Sinh[1 - t])
(---------------------------- + ((-Cos[1] + Cosh[1])
2 (-Sin[1] + Sinh[1])
(2 (-Cos[1 - t] + Cosh[1 - t]) (-Sin[1] + Sinh[1]) -
2 (-Cos[1] + Cosh[1]) (-Sin[1 - t] + Sinh[1 - t]))) /
2
((-Sin[1] + Sinh[1]) (-4 (-Cos[1] + Cosh[1]) + 4 (-Sin[1] + Sinh[1]) (Sin[1] + Sinh[1])))
) (-Sin[x] + Sinh[x])}