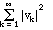 is not always
finite but that
is not always
finite but that
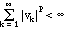 for some value
of p
for some value
of p 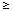 1 other than 2.
The set of all such sequences is known as the sequence space
1 other than 2.
The set of all such sequences is known as the sequence space
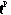 .
.
There is no inner product on 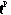 when p
when p 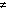 2, but there is still a
norm.
2, but there is still a
norm.
Here we define the norm and verify that it functions properly. This will require us to look at three inequalities, which are important in analysis independently of the theory of vector spaces, viz., Young's, Hölder's, and Minkowski's inequalities.
The first two of these use the concept of a dual index:
Definition IIa.1. If p is a number between 1 and infinity, then its dual index q is the number such than 1/p + 1/q = 1. A little simple calculation shows that q = p/(p-1).
Theorem IIa.1 (Young's inequality). Suppose that x and y
are numbers and p and q are dual indices. Then
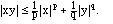
Proof. The proof is by elementary calculus. It is not hard to see that we may assume that x and y are positive, and this avoids some clutter. Fix y > 0, and find the maximum value of
xy - xp /p
by differentiating with respect to x and setting the derivative to 0. The maximizing value of x is y1/(p-1)). We conclude that
xy - xp /p
 yp/(p-1) - yp/(p-1) /p,
yp/(p-1) - yp/(p-1) /p,
which
 yq /q.
yq /q.
QED
Next suppose that v is in the sequence space
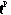 .
We claim that
we can define a norm for such
sequences by
.
We claim that
we can define a norm for such
sequences by
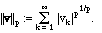 .
.
The only property of the norm that is not obvious is the triangle inequality. If there is an inner product, the triangle inequality is a consequence of the CSB inequality, which is not true for all values of p. There is, however, a generalization of the CSB inequality:
Theorem IIa.2 (Hölder's inequality). Suppose that v and w
are sequences in
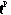 and
and
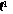 ,
and p and q are dual indices. Then
,
and p and q are dual indices. Then
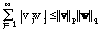 .
.
Proof. This follows from Young's inequality if we choose x and y very carefully. The good choices (again simplifying by supposing that everything is positive) are
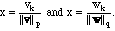 .
.
This yields
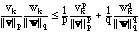
If we then sum on the index k, the right side simplifies to 1/p + 1/q
= 1, and we get Hölder's inequality when we multiply by the
denominator on the left.
QED
Finally, we use this pretty much as in the familiar case where p=2 to derive a triangle inequality for the p-norm:
Theorem IIa.3 (Minkowski's inequality). Suppose that v and w
are sequences in
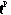 for p
for p
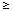 1. Then
1. Then
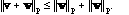 .
.
Proof. This is clear for p=1 because of the usual triangle inequality for the absolute value, so we suppose that p > 1. Then we write
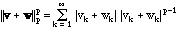
and majorize the right side by
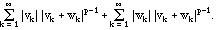 .
.
Now, on the right,
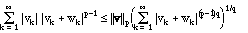 ,
,
and similarly for the second term, except with ||w|| in place
of ||v|| - the other factor is identical. We then simplify by
recalling that (p-1)q = p and collect terms. Minkowski's inequality
falls out.
QED
We remark that there are integral versions of
Hölder's and Minkowski's
inequalities, as you might expect, so that if f is a function defined
on a region 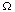 , and
, and
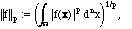
then
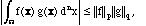
and ||f||_p defines a norm for all p
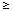 1.
1.
Link to