Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 12 January 2000
If you wish to print a nicely formatted version of this chapter, you may download the rtf file, which will be interpreted and opened by Microsoft Word. Alternatively, you may switch to the Adobe Acrobat version of this chapter.
Here are a Mathematica notebook and a Maple worksheet performing some of the calculations of this chapter.
Finally, here are some remarks for the instructor.
The other familiar vector operation we shall use, besides sums and scalar multiples, is the dot product, which we abstractly call an inner product. (We won't be concerned with analogues of the cross product, although you may see these in other courses.) You probably learned about the dot product as connected with trigonometry - the dot product of two vectors is given as the product of their lengths times the cosine of the angle between them:
(2.1)
Later you learned that this could be conveniently calculated from the
coordinates of the two vectors, by multiplying given components together and
summing: If the components of the vector v are
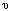 1, ...,
1, ...,
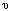 n
and those of w are
n
and those of w are
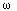 1, ...,
1, ...,
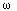 n., then
n., then
(2.2)
From the abstract point of view it is best not to begin with angle, since we don't have a good intuitive picture of the angle between two functions or matrices. Instead, we will make sense of the "angle" between functions from the connection between these formulae.
In the abstract setting, we shall denote the inner product
We shall usually call this the norm rather than the length.
An abstract inner product will share most of the properties you learned
about for the ordinary dot product:
2. Linearity :
Note: some texts define an inner product to be linear on the right side rather
than the left side. This makes no practical difference, but if there are
complex quantities, you should be careful to be consistent with whichever
convention you follow.
3. Symmetry :
(The bar denotes complex conjugate, in case these are complex numbers.)
4. Positivity :
5. The Cauchy,
Schwarz, or
Buniakovskii inequality
(depending on your nationality):
6. The triangle inequality :
is to make sense geometrically. We will shortly define an inner product for
functions. The reason we can speak of the geometry of functions is that
properties 5 and 6 follow automatically from Properties 1-4. Since this is not
at all obvious, I shall prove it below.
Definition II.1. Given an abstract vector space, an inner product
is any mapping satisfying properties 1-4 above. A vector space with an
inner product is called an inner product space.
Examples II.2.
1. The usual dot product, as defined in (2.2).
2. A modified dot product on 2-vectors. A modification of the
usual dot product
can also produce an inner product defined by
where
Actually, we could consider the vector space of n-vectors and let A be any
positive n by n matrix. (By
definition, a positive matrix is one for which the inner product so defined
satisfies Property 4 of the inner product.)
3. The standard inner product for functions.
Consider the set of functions which are
continuous on an interval a
Some fancier examples of inner products.
Theorem II.3. If V is an inner product space, then the CSB inequality (Property 5) and the triangle inequality
(Property 6) hold.
Proof (don't worry -it won't hurt you!)
The most familiar inner product space is Rn, especially with
n=2 or 3, and a brief review of some vector operations is
available as a
Mathematica notebook.
Having the CSB inequality in hand, we may now define a strange but useful idea
- the angle between two functions. Consider, for example, the interval
0
Since their inner product is
the cosine of the angle between the two functions must be
Thus the "angle" between the functions 1 and x is
Definition II.4. Two functions f and g are said to be orthogonal
if <f,g> = 0. A set of functions {fj} is orthogonal if
<fj,fk> = 0 whenever j differs from k. The set is said to be orthonormal
if it is orthogonal and ||fj|| = 1 for all j.
With the Kronecker delta
symbol,
Examples II.5.
1. Integral tables, mathematical software, integration by parts (twice),
substitution with the cosine angle-sum rule, and rewriting trigonometric
functions as complex exponentials can all be used to evaluate integrals such as
Any or all of these methods will lead to the same conclusion, viz.:
The set of functions
is orthogonal on the
interval [0,L], and to turn it into an orthonormal set, we normalize the
functions by multiplying by the appropriate constant:
2. Similarly,
is orthonormal on the interval [0,L], and we can even include another function,
the constant:
3. We can mix the previous two sets to have both sines and cosines as long as
we leave out all of the odd coefficients:
is also an orthonormal set. This one is the basis of the usual
Fourier series,
and is perhaps the most important of all our orthonormal sets. By the way,
we do not claim that the functions in (2.6), (2.7), and (2.8) are orthogonal
to functions in the other sets, but only separately among themselves. For
instance,
4. Recall that by Euler's formula, exp(i
have many useful properties, including
and
is an orthonormal set on [0,L].
For later purposes, we observe here that the sets of functions (2.5)-(2.9) are
each orthogonal on any interval [a,b] with L = b-a.
Before finishing this section we need two more notions about vectors and
functions, thought of as abstract vectors. The first is distance. With the
standard inner product, we would like to define the distance between two
functions f and g as the
L2 norm of f - g:
This turns out to be a familiar quantity in data analysis, called the
root-mean-square, or r.m.s., deviation. It is a convenient way of
specifying how large the error is when the true function f is replaced by a
mathematical approximation or experimentally measured function g. It is always
positive unless f = g almost everywhere.
Definition II.6. Almost everywhere is a technical
phrase
meaning that f and g differ for sufficiently few values of x that all integrals
involving f have the same values as those involving g. Such a negligible set
is called a null set.
For most practical
purposes we may regard f and g as the same functions, and write:
f = g a.e.
A typical example is where a function is discontinuous at a point and some
arbitrary decision is made about the value of the function at the
discontinuity. Different choices are still equal a.e. Much more exotic
possibilities than this typical example can occur, but will not arise in this
course.
The second notion we generalize from ordinary vectors is that of projection.
Suppose that we have a position
vector in three dimensions such as v = (3, 4, 5)
Model Problem II.7. We wish to find the vector in the plane spanned by
(1,1,1) and (1,-1,0), which is the closest to v = (3,4, 5) .
Solution. We solve this problem with a projection. The projection of a vector
v onto v1 is given by the
formula:
Notice that this points in the direction of v1 but has a length equal to ||v||
cos(theta), where
theta is the angle between v and v1. The length of v1 has
nothing to do with the result of this projection - if we were being very careful, we would
say that we were projecting v onto the
direction determined by v1, or onto the
line through v1.
For similar reasons we notice that the vector v1 could be normalized
to have length 1, so that the
denominator can be ignored - it is 1. In our example,
(Here we write the vectors as column vectors because the projection
operator is equivalent to a 3 by 3 matrix multiplying them.)
If the
basis for the plane consists of orthogonal vectors v1 and v2, as in
our example, then the projection into the plane is just the sum of the
projections onto the two vectors:
In our example,
Calculations like these are easily done with software; see the
Mathematica notebook or the
Maple worksheet
Model Problem II.8. We wish to find a) the vector in the
plane spanned
by (1,1,1) and (1,2,3), which is the closest to v = (3, 4, 5)
and b) the vector in the plane closest to (1,-1,0) .
Solution. This is similar to the previous problem, except that the vectors defining
the plane are not orthogonal. We need to replace them with a different pair of
vectors, which are
linear combinations
of the first, but which are orthogonal.
(We'll do this later systematically, with the Gram-Schmidt
method.)
The formula (2.11) is definitely wrong if the
vectors vn are not orthogonal (problem II.8).
After finding the new pair of vectors, however, the solution will
be as before - just sum the projections onto the orthogonal basis vectors.
There is more than one good choice for the pair of orthogonal basis vectors.
If we solve the vector equation
for
The projection of (3,4,5) into the plane is the sum of its
projections onto these vectors, i.e.,
Perhaps it looks strange to see that the projection of the vector
(3,4,5) is itself, but the interpretation is simply that
the vector was already in the plane before it was projected.
In general a vector will be moved (and shortened) when it is projected
into a plane, and we can see this when we project (1,-1,0):
Now that we have a vector in the plane, if we project again, it won't move. Algebraically, projections satisfy the equation
P2 = P .
For example, if we wish to find the multiple of sin(3x) which is closest to the function x on the interval 0 < x <
The projection of a vector/function onto its own
direction will be the same as the vector/function itself.
Now consider what we mean when we project a function onto the
constant function 1. This should be the best
approximation to f(x) consisting of a single number. What could
this be but the average of f? Indeed, the projection formula gives us
which is familiar as the average of a function.
Model Problem II.9. Consider the set of functions on the
interval -1
Solution. The calculations can be done with Mathematica (see
notebook)
or Maple (see
worksheet) if you prefer.
Conceptually, the calculations are closely analogous to those of
Model Problem II.8.
First let us ask whether the three functions are orthogonal. Actually, no.
The function x is orthogonal to each of the other two, but 1 and
x2 are not orthogonal. We can see this immediately because x is odd,
while 1 and x2are both even, and both positive
a.e.
A more suitable function than x2
would be x2 minus its projection
onto the direction of 1, that is, x2 minus its average,
which is easily found to be 1/3. The set of functions
{1, x, and x2 - 1/3} is an orthogonal set, as you can check.
Then we can project cos(¹x/2) onto the
span of the three functions 1, x, and x2 - 1/3:
The best quadratic approximation to
cos(
For comparison, here is a plot which shows the
Taylor approximation
as well as the original and the best quadratic:
Step 1. Replace g1...gn by an orthogonal set with the same span. (A systematic way to do this, the
Gram-Schmidt
procedure, is described below.) Let's call the orthogonal set h1...hn.
Perhaps the most important functional approximation uses the
Fourier functions
(2.8),
as we shall learn to call them. The coefficients of these functions in the projection are called Fourier coefficients, and the approximation is as follows:
The right side should be the projection of f(x) on
the span of the sines and cosines (including the constant) on
the right. To get the coefficients we use the analogue of the formula
(2.10).
For example,
In other words, the formula for the coefficients am must be:
As mentioned above, the projection of f onto a constant function is its
average.
Finally, the
analogous calculation for the sines gives:
Formulae (2.13)-(2.15) will be the basis of the Fourier series in the next
section.
The notions of best approximation and projection in function space are at the heart
of filtering theory. A filtered signal is nothing other than a function that has been
projected in some way to remove certain frequencies or some undesired characteristics
such as noise.
(Some further remarks about filtering and signal processing.)
Constructing orthonormal sets. It is often convenient to have
orthonormal, or at least orthogonal sets. These are analogous to the usual basis
vectors for the plane or for 3-space (denoted R3), but you may
recall that there are many choices of orthogonal bases. For instance, you may
have unit vectors oriented along the x,y, and z axes, but someone else may have
unit vectors oriented along a rotated set of axes. Although we shall first
concentrate on the set (2.8) as a basis for a vector space of functions, the
other sets of orthonormal functions (2.5)-(2.7) and (2.9) will be useful later
for the same purpose. The choice among these sets is analogous to the choice
of different bases for R3.
But how do we come up with a basis in the first place? Suppose you are given
several vectors, such as v1,2,3 = (1,0,0), (1,1,0), and (1,1,1), and you want
to recombine them to get an orthonormal, or at least orthogonal set. You can
do this by projecting away the parts of the vectors orthogonal to each other.
The systematic way of doing this is called the
Gram-Schmidt procedure, and it
depends a great deal on the order in which it is done.
Model Problem II.10. Find an orthonormal set with the same span as
v1,2,3 = (1,0,0), (1,1,0), and (1,1,1), beginning with w1 = v1 = (1,0,0).
(We rename it because it is the first vector in a new set of recombined
vectors.)
Solution. The next vector v2 is not orthogonal to v1, so we subtract off the
projection of v2 onto the direction of v1:
For w3, we begin with v3 and project away the parts in the plane spanned by
v1 and v2, which is the same as the plane spanned by w1 and w2. We find
the standard basis vector
Notice that the results are different if we take the same vectors in a different
order:
Model Problem II.11. Find an orthonormal set with the same span as
v1,2,3 = (1,0,0), (1,1,0), and (1,1,1), beginning with v3.
Solution. Fist let's turn v3 into a unit vector:
For the second unit vector we could take v2 and project away the part pointing
along v3, getting
which we can normalize as
Finally, taking v1, projecting out the components in these directions, and
normalizing, gives us the vector
Model Problem II.12. Construction of the
Legendre polynomials. (See the
Mathematica notebook or
Maple worksheet for a computer-assisted discussion.)
Let us
consider the interval
-1
Let us denote the set of orthogonal polynomials we get using the Gram-Schmidt
procedure on the power functions (in this order) p0, p1, p2, .... These are
important in approximation theory and differential equations, and are known as
the normalized Legendre polynomials.
Beginning with the function x0 = 1, after normalization we find
The next power is x1 = x. Since x is already orthogonal to any constant function, all we do is normalize
it:
To make x2 orthogonal to p0 , we need to subtract a constant:
x2 - 1/3. Because of symmetry, it is already orthogonal to p1, so
we don't worry about p1 yet, and just normalize:
Similarly, when orthogonalizing x3 we need to project out x but not
1 or x2. We find x3 - 3x/5,
or, when normalized:
etc.
By the way, Legendre
polynomials are traditionally not normalized as we have
done, but rather are denoted Pk(x) and scaled so that Pk(1) = 1.
The normalization for Legendre polynomials of arbitrary index is such that
pn(x) = (n + 1/2)1/2 Pn(x).
Most special
functions are known to Mathematica and Maple, so calculations with them
are no more difficult than calculations with sines and cosines. (See the
Mathematica notebook
or
Maple worksheet.)
Sometimes it is not possible to define an inner product, but there is
still some useful geometry which depends only on the
norm, and sometimes on a slightly more complicated version of the
CSB inequality, known as
Hölder's inequality. (Further discussion.)
II.1. Find the norms of and "angles" between the following functions
defined for
-1
1, x, x2,
cos(
II.2. Verify the inner product of
Example II.2.5 for 2x2 matrices. Find all
matrices orthogonal to
Do they form a subspace of the 2 by 2
matrices? If so, of what dimension?
(Selected solutions by
Mathematica are available
in Mathematica format
or in
rtf format, which is readable by MS Word).
II.3. It was remarked
above that the projection operator on
ordinary 3-vectors is equivalent to a matrix. What is the matrix for the
projection onto (1,2,-3)? What is the matrix for the projection onto the
plane through the origin determined by the vectors
(1,2,-3) and (-2,0,0)?
II.4. Use the Gram-Schmidt procedure to construct other orthonormal sets
from the basis vectors
v1,2,3 given in the text, taken in other orders. How
many distinct basis sets are there?
II.5. Find the first 8 normalized Legendre polynomials.
II.6. a) Calculate the
Taylor series for
cos(
b) Use the Legendre polynomials to find the polynomial of degree 4 which is
the best approximation to
cos(
c) On a single graph, sketch
cos(
II.7. In each case below, find a) the multiple of g which is closest in the
mean-square sense
to f, and b) a function of the form f -
(i)
f(x) =
sin(
(ii)
f(x) =
sin(
(iii)
f(x) = cos(
(iv) f(x) = x2 - 1, g(x) = x2 + 1,
-1
(Selected solutions by
Mathematica are available
in Mathematica format
or in
rtf format, which is readable by MS Word).
II.8. Show with explicit examples that the formula
(2.11) is definitely wrong if the vectors vn are not
orthogonal.
Link to
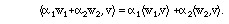


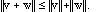 (2.4)
(2.4)
We need Property 5 if an inner product is to correlate with Eq. (2.1), and we
need Property 6 if the length
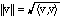
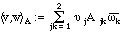
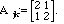
 x
x
 b.
Then the standard inner product on them is the integral:
b.
Then the standard inner product on them is the integral:
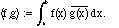
Another name for this is the L2 inner product. We can use it for
functions with discontinuities and even singularities, so long as the singularities
are not too strong. The most general set of functions, defined on a set
 , for which this inner
product is defined is known as
the set of square-integrable functions, denoted
L2(
, for which this inner
product is defined is known as
the set of square-integrable functions, denoted
L2( ).
).
 x
x L
and the functions f(x) = 1 and g(x) = x. With the standard inner
product, we first calculate their "L2" norms:
L
and the functions f(x) = 1 and g(x) = x. With the standard inner
product, we first calculate their "L2" norms: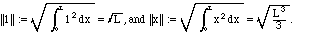
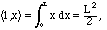
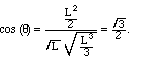
 /6 radians. The most
useful angle to deal with, however, is a right angle:
/6 radians. The most
useful angle to deal with, however, is a right angle: jk = 0
when j differs from k, and
jk = 0
when j differs from k, and
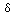 kk = 1, orthonormality
can be expressed as <fj,fk> =
kk = 1, orthonormality
can be expressed as <fj,fk> =
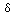 jk.
jk.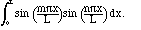
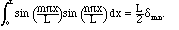 (2.5)
(2.5)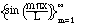
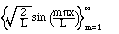 (2.6)
(2.6)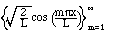 (2.7)
(2.7)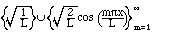


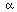 ) := ei
) := ei
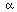 := cos(
:= cos(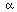 ) + i sin(
) + i sin(
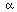 ). The complex trigonometric functions
). The complex trigonometric functions
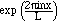
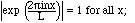
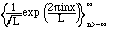 (2.9)
(2.9)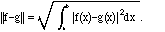
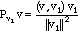 (2.10)
(2.10)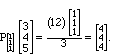
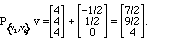
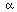 we get
we get 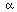 = 2, so a suitable second
vector which is orthogonal to (1,1,1) is
(-1,0,1).
= 2, so a suitable second
vector which is orthogonal to (1,1,1) is
(-1,0,1).
We shall make these same calculations in function space to find the best
mean-square
fit of a function f(x) by a nicer expression, such as the functions in
(2.8) or polynomials.
This can be automated with Mathematica
(see notebook) or Maple
(see worksheet). The formula simply replaces
the dot product with the standard inner product:
 , we find:
, we find:
 x
x 1
We wish to find the function in the span of 1, x, and x2,
which is the closest to f(x) = cos(
1
We wish to find the function in the span of 1, x, and x2,
which is the closest to f(x) = cos(
 x/2) .
In other words, find
the best quadratic fit to the function f in the mean-square sense. In
Exercise II.6 you are asked to compare a
similar global polynomial approximation to this function with the
Taylor series.
x/2) .
In other words, find
the best quadratic fit to the function f in the mean-square sense. In
Exercise II.6 you are asked to compare a
similar global polynomial approximation to this function with the
Taylor series.
 x/2) on the interval -1 < x < 1 is the
sum of these three functions. Here is a graph showing the original
function and its approximation:
x/2) on the interval -1 < x < 1 is the
sum of these three functions. Here is a graph showing the original
function and its approximation:
The general algorithm for finding the best approximation to a function is as follows.
Suppose that we want to find the best approximation to f(x),
a  x
x  b, of the form
a1g1(x) + a2g2(x) + ... + a1ngn(x),
where g1...gn are some functions with nice
properties - they may oscillate with definite frequencies, have simple shapes, etc.
They could be chosen to capture the important features of f(x), while possibly
simplifying its form or filtering out some noise.
b, of the form
a1g1(x) + a2g2(x) + ... + a1ngn(x),
where g1...gn are some functions with nice
properties - they may oscillate with definite frequencies, have simple shapes, etc.
They could be chosen to capture the important features of f(x), while possibly
simplifying its form or filtering out some noise.
Step 2. Project f onto each of the hk.
Step 3. Sum the projections. If P denotes the span of g1...gn, then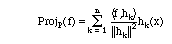 (2.12)
(2.12)
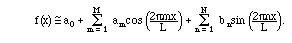
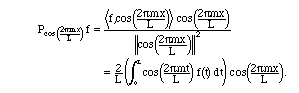
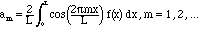 (2.13)
(2.13)
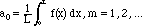 (2.14)
(2.14)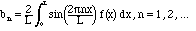 (2.15)
(2.15)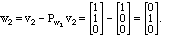
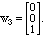
A computer-based solution, using either a
Mathematica notebook or a
Maple worksheet to do the
work of orthogonalizing for us
is also available.
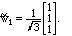
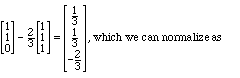
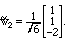
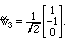
Again, a computer-based solution
using either a
Mathematica notebook or a
Maple worksheet is available.
Guess what's coming? The same procedure with sets of functions!  x
x  1,
and find a set of orthonormal
functions which are more mundane than the trigonometric functions, namely the
polynomials. We begin with the power functions 1, x, x2,
x3, .... Some of these are orthogonal because some are even
functions and others are odd, but they are not all orthogonal to one another.
For instance,
1,
and find a set of orthonormal
functions which are more mundane than the trigonometric functions, namely the
polynomials. We begin with the power functions 1, x, x2,
x3, .... Some of these are orthogonal because some are even
functions and others are odd, but they are not all orthogonal to one another.
For instance,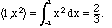
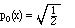
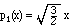
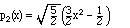
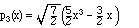
Exercises.
 x
x 1. (In the case of complex quantities, the "angle" is
not so meaningful, but you can still define the cosines of the angles.) Use
the standard inner product:
1. (In the case of complex quantities, the "angle" is
not so meaningful, but you can still define the cosines of the angles.) Use
the standard inner product: x),
exp(i
x),
exp(i
 x)
x)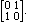
 x/2) about the point
x=0, up to the term with x4. (Go to x6 if you choose to
use software to do this problem.)
x/2) about the point
x=0, up to the term with x4. (Go to x6 if you choose to
use software to do this problem.) x/2) for
-1
x/2) for
-1 x
x 1.
1. x/2) and these two approximations.
x/2) and these two approximations.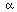 g which is orthogonal to f. If for some reason this
is not possible, interpret the situation geometrically.
g which is orthogonal to f. If for some reason this
is not possible, interpret the situation geometrically. x), g(x) = x,
0
x), g(x) = x,
0  x
x  1
1 x), g(x) = x, -1
x), g(x) = x, -1  x
x  1
1 x), g(x) = x,
-1
x), g(x) = x,
-1  x
x  1
1 x
x  1
1