Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 9 October 2000.
Many of the calculations in this chapter are available in a Mathematica notebook or Maple worksheet.
(Some remarks for the instructor).
This is an interlude from our study of wave equations by the method of separation of variables. For the standard wave equation
where c is a constant, there is a completely different-looking method of solution, due to the French mathematical physicist Jean le Rond d'Alembert. Indeed, the idea behind the method of this chapter can be the subject of an entire course on the method of characteristics. (If you wish, you can access James V. Herod's text on this subject.)
Suppose
 is a function of one variable z, but we set z = x + ct.
Then
is a function of one variable z, but we set z = x + ct.
Then
 (x+ct) represents a fixed wave-form which moves to the left at speed x as
time goes on. Provided that
(x+ct) represents a fixed wave-form which moves to the left at speed x as
time goes on. Provided that
 can be differentiated twice, it is automatically
a solution of the wave equation, which we can
rewrite as in chapter VI
in terms of a
wave operator
as
can be differentiated twice, it is automatically
a solution of the wave equation, which we can
rewrite as in chapter VI
in terms of a
wave operator
as
 u = 0.
(Recall that by definition,
u = 0.
(Recall that by definition,
.
for any t,x and suitable f.) It is not hard to verify this fact with the chain rule, and you may recall that we saw a particular example in chapter VI.
Since the wave equation is linear, given any two
functions of a single variable, which can be differentiated twice, the
expression
 (x+ct)+
(x+ct)+
 (x-ct) is
also a solution. Suppose now that we have an infinitely long string, and
initial conditions of the usual form:
(x-ct) is
also a solution. Suppose now that we have an infinitely long string, and
initial conditions of the usual form:
We do not need boundary conditions for this problem, although sometimes it is
physically important to have "boundary conditions at infinity" that as x ->
±
 , u -> 0, so that the wave energy is finite.
, u -> 0, so that the wave energy is finite.
Can we always find a solution of the form
u(t,x) =
 (x+ct) +
(x+ct) +
 (x-ct),
(7.1)
(x-ct),
(7.1)
which solves this initial-value problem? Yes indeed! For simplicity, let us begin with the case where g(x) := 0. Substituting t=0 shows that
 (x)+
(x)+  (x) = f(x)
(x) = f(x)
while, since ut(0,x) = c
 '(x+ct)- c
'(x+ct)- c  '(x-ct),
'(x-ct),
c
 '(x)- c
'(x)- c  '(x) = 0.
'(x) = 0.
This last equation can be integrated to give  (x) =
(x) =
 (x)+ C, but
we take this constant to be zero (if f(x) -> 0 at infinity, this is forced
on us by the BC at infinity). Thus:
(x)+ C, but
we take this constant to be zero (if f(x) -> 0 at infinity, this is forced
on us by the BC at infinity). Thus:
 (x) =
(x) =  (x) = f(x) /2.
(x) = f(x) /2.
and
u(t,x) = f(x+ct) /2 + f(x-ct) /2.
Model Problem VII.1. Let the initial displacement f(x) be Exp(-x2), and let the initial velocity g(x) = 0. Then the solution in the future is
We should see the initial bump break into the superposition of two bumps of half the height, one moving to the right and one to the left. Here are some snapshots at different times of the displacement as a function of x:
Next, let's turn the tables and suppose that f(x) = 0 but g(x) differs from 0. Putting in t=0, we see that
 (x) = -
(x) = - (x),
(x),
while
c
 '(x)- c
'(x)- c  '(x) = 2 c
'(x) = 2 c
 '(x) = g(x).
Clearly, then,
'(x) = g(x).
Clearly, then,
.
The constant of integration is not specified, but since the full solution is of the form
f(x+ct) - f(x-ct) ,
it will drop out of the solution.
The solution to (WE) with these IC is:
If, for example, c=1 and
Then a calculation shows that
Here are some snapshots of the solution:
The solution with the given initial conditions keeps moving upward.
The solution with both initial conditions
u(0,x) = f(x)
ut(0,x) =g(x)
is just the sum of the previous two solutions, because of the superposition principle:
Model Problem VII.2. Find the solution of the wave equation for unrestricted x, with c=1 and initial conditions f(x) = sin(4 x), g(x) = x2-1/3
Solution. Using software to calculate with formula (7.2), the answer (see Mathematica notebook or Maple worksheet) is:
Although the formula for the solution is fairly simple, the wave forms it describes can be complicated. For example, at unit time steps beginning at t=0, this solution looks as follows:
Here is the trick. Suppose that we have (say) DBC at 0, and we watch the vibrating string through a window where we can see only what is going on at x > 0. We can't tell whether the string is actually clamped down at 0, but the height of the string just happens to be 0 at 0 (at all times). The way we can arrange this is to exploit symmetries. When we formalize this idea in a later chapter and a somewhat different context, it will be called the method of images
If f(x) and g(x) are defined on -
 < x <
< x <
 and are
even about the point 0 (i.e., f(-x) = f(x) and g(-x) = g(x)), then the solution
by d'Alembert's method will also be even, since
and are
even about the point 0 (i.e., f(-x) = f(x) and g(-x) = g(x)), then the solution
by d'Alembert's method will also be even, since
The substitution in the middle line is r=-s.
It works the same way if f and g are even about some point other than 0. Likewise if f and g are odd, then so is the solution (see Exercise 1).
Model Problem VII.3. Solve the wave equation (with c=1) for 0 < x
<
 with the following initial and boundary conditions. Use the
superposition principle and the uniqueness theorem for this problem to simplify
your analysis.
with the following initial and boundary conditions. Use the
superposition principle and the uniqueness theorem for this problem to simplify
your analysis.
a) u(0,x) = 0, ut(0,x) = 0, u(t,0) =t2.
b) u(0,x) = sin(x), (v(0,x) = 0, u(t,0) = t2.
c) u(0,x) = 0, ut(0,x) = 0, ux(t,0) = t exp(-t).
Solutions.
a) u(0,x) = 0, ut(0,x) = 0, u(t,0) = t2.
The uniqueness theorem for this problem tells us that it has only one solution. The point of uniqueness theorems is often lost on students, but in fact they can be extremely practical: If you can solve a different problem from the one which was posed, but it happens to satisfy all the conditions, then it must be the solution of the original problem, too.
In this case, we know how to solve the wave equation if there is no boundary and we are given initial conditions for all x. D'Alembert discovered that the general solution in that case is a superposition of a wave moving to the right and a wave moving to the left. The shapes of the moving waves can be arbitrary until they are fixed by the boundary conditions.
With this in mind, imagine a string with -
 < x <
< x <
 carrying with a rightward moving wave, which happens to be of zero amplitude
when t = 0 and x > 0. In other words, u(t,x) =
carrying with a rightward moving wave, which happens to be of zero amplitude
when t = 0 and x > 0. In other words, u(t,x) =  (x-t), where
(x-t), where
 (x-0) =
(x-0) =  (x) = 0 when x > 0. This satisfies the initial
conditions, so it must be the boundary condition at x=0 which determines the
unknown function y: Putting x=0, we see that
(x) = 0 when x > 0. This satisfies the initial
conditions, so it must be the boundary condition at x=0 which determines the
unknown function y: Putting x=0, we see that
 (0-t) = t2 for all t > 0
(0-t) = t2 for all t > 0
We now know  (x) = for all values of x, because given any negative x , we
can substitute x = -t and use this last observation to find that
(x) = for all values of x, because given any negative x , we
can substitute x = -t and use this last observation to find that  (x) =
(-x)2 = x2. In the traveling wave, we replace x by x-t, so the solution
is:
(x) =
(-x)2 = x2. In the traveling wave, we replace x by x-t, so the solution
is:
u(t,x) =  (x-t) = (x-t)2 when 0 < x <= t, and
otherwise 0.
(x-t) = (x-t)2 when 0 < x <= t, and
otherwise 0.
b) u(0,x) = sin(x), ut(0,x) = 0, u(t,0) = t2.
Let us think about the superposition principle here to simplify things, rather than beginning the whole analysis at the beginning. A linear combination of solutions of the wave equation is again a solution of the wave equation, but the boundary condition is non-homogeneous. This means that we can't just add two solutions such that u(t,0) = t2; if we did the boundary condition satisfied by the sum would be 2 t2, not t2. If, however, we added a function satisfying our boundary condition to one having a zero Dirichlet condition, the sum would equal t2 at the boundary. This suggests the following strategy:
Step 1, Solve problem a), with u(0,x) = 0, which we did above.
Step 2, Solve a simpler problem, the wave equation with
b') u(0,x) = sin(x), ut(0,x) = 0, u(t,0) = 0.
Step 3. Add the two solutions.
Since the sum solves the wave equation and the initial and boundary conditions, it is the one and only correct answer to problem b).
Here is how to solve b'). If we extend x to -
 and u(0,x) = sin(x)
there, then our initial condition would be odd, and we might expect that by
symmetry, u(t,0)= 0 when t > 0. The solution of this problem, by
d'Alembert's method, is:
and u(0,x) = sin(x)
there, then our initial condition would be odd, and we might expect that by
symmetry, u(t,0)= 0 when t > 0. The solution of this problem, by
d'Alembert's method, is:
(1/2) (sin(x+t) + sin (x-t) ),
and when x=0, this is (1/2) (sin(t) + sin (-t) ), which is indeed zero, since the sine is an odd function. It may also help to notice that by the sine-sum formula,
(1/2) (sin(x+t) + sin(x-t)) = sin(x) cos(t)
The solution to problem b) can be written:
u(t,x) = (x-t)2 + sin(x) cos(t), when 0 < x <= t, and
sin(x) cos(t), otherwise.
c) u(0,x) = 0, ut(0,x) = 0, ux(t,0) = t exp(-t).
We can solve this problem just as for problem a), by imagining that the
solution is a traveling wave coming from the left of 0, but which hasn't
disturbed the string at x>0 before it arrives at t=0. Thus u(t,x) =
 (x-t), where
(x-t), where
 (x-0) =
(x-0) =
 (x) = 0 for x > 0.
(x) = 0 for x > 0.
The difference is the boundary condition. This time we know that
ut = - y'(x-t), and at time 0, we have
-  '(0-t) = t exp(-t).
'(0-t) = t exp(-t).
Perhaps it is best here to change variables so that x = -t. Then:
- '(x) = -x exp(x),
'(x) = -x exp(x),
so, by integrating, we find that
 (x) = (x-1) exp(x) + C.
(x) = (x-1) exp(x) + C.
The condition that the solution will be 0 when x = 0 fixes the conmstant, so we get
 0 (and 0 for x-t > 0).
0 (and 0 for x-t > 0).
It is easy to check the boundary condition, whether by hand or with software.
Model Problem VII.4. Suppose that g(x) = 0, but f(x) = x(1-x), 0 < x < 1. Extend these functions to all of x and thereby solve the initial-boundary-value problem with these initial conditions and zero Dirichlet boundary conditions at 0 and 1.
Solution. We need to extend f and g so as to be odd around both 0 and 1.
Obviously, we extend g(x) as 0 for all x, but f(x) is a little trickier For x
from -1 to 0, we change f(x) to -f(-x).
Maple or Mathematica can be invoked to show
what is going on (see the worksheet
or the
It looks much like a sine function, but numerically it isn't. We could go on
like this all day, or we could use modular arithmetic
as represented by the commands
floor and frac in
Maple or the commands
Floor and FractionalPart in
Mathematica.
(Some programming languages use int and frac.)
As shown in the Maple
worksheet or the
Mathematica notebook for this chapter, you can see
how to
piece a function together so that it is periodic with, say, period 2, as
shown here:
With the software, we can then solve the IBVP with
formula (7.2):
With software it is possible to animate this and see the standing wave motion.
Notice that the wave does not simply jiggle up and down; its shape is changing,
too.
.
The wave equation is the prototype for a class of partial differential
equations, the hyperbolic equations. Other ones exhibit wave motion,
although the speed may vary and dispersion and dissipation may occur. (In more
ordinary language, the waves may spread and die down.) Another feature of the
hyperbolic equations is that they are quite tolerant of irregularities. The
general solution (7.1) makes no reference to the differentiability of
 and
and  , and indeed, even if
, and indeed, even if
 and
and  are discontinuous, that
formula has a reasonable interpretation as a superposition of traveling waves.
Such an expression is referred to as a weak or generalized
solution of the wave equation, and is important in applications because it
describes shock waves, sonic booms, etc.
are discontinuous, that
formula has a reasonable interpretation as a superposition of traveling waves.
Such an expression is referred to as a weak or generalized
solution of the wave equation, and is important in applications because it
describes shock waves, sonic booms, etc.
A weak solution can be defined formally by integration by parts. Suppose that
a function of the form (7.1) is put into an inner product with another function
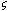 t,x) which
t,x) which
 < x,t
<
< x,t
<
 .
.
I will refer to the region on which
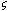
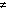 0, together with the boundary
of this region, as its
support. If u(t,x) is differentiable twice with respect
to t and x (and the derivatives are continuous functions), and A denotes the
wave operator defined above,
then integration by parts shows that
0, together with the boundary
of this region, as its
support. If u(t,x) is differentiable twice with respect
to t and x (and the derivatives are continuous functions), and A denotes the
wave operator defined above,
then integration by parts shows that
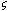 ,u> = <
,u> = <
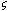 , A u> = 0
(7.4)
, A u> = 0
(7.4)
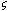 . The functions
. The functions
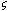 are referred to as test
functions, and you can think of (7.4) as a way of testing whether u is a
solution of the wave equation without differentiating it directly.
are referred to as test
functions, and you can think of (7.4) as a way of testing whether u is a
solution of the wave equation without differentiating it directly.
Definition. A function u which satisfies (7.4) for all test functions is a weak solution of the wave equation.
The method of d'Alembert works in a modified form for other hyperbolic, and even parabolic, partial differential equations, and is more generally known as the method of characteristics. Instead of simple, traveling waves, the solutions consist of waves which travel along special curves, and which can have variable speeds and can change their shapes. If the equations are not linear, the waves will not satisfy the superposition principle, but the method of characteristics is less closely tied to linearity than is the method of separation of variables.
VII.1. As in eq.(7.2), verify that
a) If f and g are even about a general point x=a, i.e., f(2a - x) = f(x) and g(2a - x) = g(x), then so is the d'Alembert solution with these initial conditions.
b) If f and g are odd about a general point x=a, i.e., f(2a - x) = -f(x) and g(2a - x) = -g(x), then so is the d'Alembert solution with these initial conditions.
VII.2. Use the int and frac functions to extend the function f(x) = x
(1-x), 0<=x<=1, to all -
 <x<
<x<
 such that
such that
 <x<
<x<
 such that
such that
VII.4. Show that the solution obtained with d'Alembert's method with boundary conditions is equivalent to the solution we got by separation of variables, even though they look quite different. You will need to use trigonometric identities.
VII.5. Consider the wave equation on the whole line -
 < x
<
< x
<
 , but change variables so that z = x+ct and w = x-ct. Show
that the wave equation becomes
, but change variables so that z = x+ct and w = x-ct. Show
that the wave equation becomes
uzw = 0.
Derive d'Alembert's solution from this equation, by integrating it first with respect to z and then with respect to w. (Hint: Since the partial derivative with respect to z means that w is being held temporarily fixed, if you integrate something with respect to z, the "constant" of integration may be different for different values of w. In other words, instead of a constant of integration you get a function of w. Similarly for integrating partial derivatives with respect to z.
VII.6. Derive (7.4)
VII.7. Show that if u(t,x) =
 (x-ct) for a function
(x-ct) for a function
 which
is merely assumed
piecewise continuous
, then u is a weak solution of the wave
equation.
VII.8. Solve the modified wave equation
which
is merely assumed
piecewise continuous
, then u is a weak solution of the wave
equation.
VII.8. Solve the modified wave equation
utt = uxx - (1/4) ut - 32
with IC:
u(0,x) = sin(2 x)
ut(0,x) = 0
and BC:
u(t,0) = 0
u(t,2p) = 1.
(You will want to use ideas from both this chapter and chapter VI to solve this nonhomogeneous problem.) VII.9. Solve the wave equation
utt = uxx
for 0 < x
< , 0
< t
<
, 0
< t
< , with initial conditions
, with initial conditions
 .
.