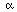
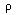 (x,y),
(PE)
(x,y),
(PE)
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 7 May 2000
If you wish to print a nicely formatted version of this chapter, you may download the rtf file, which will be interpreted and opened by Microsoft Word or the pdf file, which will be interpreted and opened by Adobe Acrobat Reader.
In this chapter we separate variables in order to solve the wave equation. Many of the calculations are available in the format of a Mathematica notebook or Maple worksheet.
(Some remarks for the instructor).
utt = c2 uxx; (WE)
the heat equation, also known as the diffusion equation,
ut = k uxx; (HE)
and the potential equation, also known as Poisson's equation,
uxx + uyy =
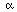
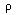 (x,y),
(PE)
(x,y),
(PE)
where
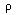 is
a given function corresponding in electrostatics to a charge
distribution, and the other quantities c, k , and
is
a given function corresponding in electrostatics to a charge
distribution, and the other quantities c, k , and
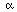 are physical
constants. Often there is no charge in the region where you want to measure a
potential , and (PE) reduces to Laplace's equation
are physical
constants. Often there is no charge in the region where you want to measure a
potential , and (PE) reduces to Laplace's equation
uxx + uyy = 0. (LE)
One thing you are likely to notice if you take several advanced courses in science or engineering is that these same equations arise in many different contexts. The function u may have a different interpretation in each incarnation, but the mathematics remains the same. For example, the function u in (PE) or (LE) might be an electric potential, a magnetic potential, the height of a taut membrane, or the potential of the velocity field in a fluid.
The reason these equations arise again and again is that they are the most symmetric second order partial differential equations that can be written down. Fundamental physical principles usually do not involve derivatives of higher than second order. If a physical model is isotropic, has a superposition principle, and is based on fundamental physical principles, it is very likely to lead to an equation of one of these forms.
The mathematics and physics of the three types of equations differ in important ways, and lead to a classification of the equations as hyperbolic (WE), parabolic (HE), and elliptic (PE/LE). Other second-order equations of a given type will share the qualitative features of our three models.
We shall begin our study of the method of separation of variables with the one-dimensional wave equation, which controls the vibrations of a taut string (see derivation) and some other phenomena. The wave equation (WE) written can be written with the aid of a wave operator
so that (WE) is the equation for the kernel of this operator. This operator is also known as the d'Alembertian. The wave equation is a linear, homogeneous equation, so the superposition principle holds for its solutions. If we can find some solutions u1, ..., uk, then any linear combination of these solutions is again a solution. We also classify it as "second-order," since derivatives up to second order occur, but no higher-order derivatives. This will be the case for the great majority of PDE's in this class.
We shall solve the wave equation in two entirely different ways. The first method is known as separation of variables. Let's set c = 1 for convenience and test out the wave operator by calculating its action on some representative functions:
Somewhat surprisingly,, the second seemingly arbitrary
function
is a solution of
(WE)! As we shall see,
there are lots of solutions, and several strategies for finding them.
With the method of separation of variables, we try to find solutions of a
special form, u = T(t) X(x),
called
u(t,0) = 0, u(t,L) = 0 (DBC)
This means that the string is fastened at two ends, x=0 and x=L. Actually, if we assigned some other fixed values to u besides 0 at the end points, we could just redefine the dependent variable:
If u(t,0) = a, u(t,L) = b,
then define v := u(t,x) - a - (b-a) x/L.
The function v will still solve the wave equation, vtt - vxx, but it will have the simpler boundary conditions (DBC).
When we act on a product T(t)X(x) with the wave operator and divide the result by T(t)X(x), we get
(More details in these calculations are given in the accompanying Mathematica notebook or Maple worksheet.) If u solves the wave equation, this expression must be zero. (We could quibble about what happens when T or X = 0, but that would either mean that u is the uninteresting "trivial" solution or else the problem occurs only at isolated values of x and t.) Thus
T''/T = X''/X.
Since the left side of this is independent of x and the right side is independent of t,
both sides must in fact be a constant. We don't know its value yet, so let us
call it -
 . It will turn out to be negative.
. It will turn out to be negative.
-X''(x) =
 X(x)
(6.1)
X(x)
(6.1)
This sort of equation is similar to a matrix-vector equation in linear algebra
and is called an eigenvalue equation.
The function X and the number
 are both unknown, and are called and eigenfunction and eigenvalue. We do not
allow the possibility X(x) = 0 for all x. While it is always a solution for
all u, it is not useful. By definition, an eigenfunction must be a nonzero
solution of an equation like (6.1). Along with (6.1) we have the boundary
conditions
are both unknown, and are called and eigenfunction and eigenvalue. We do not
allow the possibility X(x) = 0 for all x. While it is always a solution for
all u, it is not useful. By definition, an eigenfunction must be a nonzero
solution of an equation like (6.1). Along with (6.1) we have the boundary
conditions
X(0) = X(L) = 0 (6.2)
and this will restrict the
 's for which
(6.1) has nonzero solutions. Eq. (6.1)
is an elementary ordinary differential equation with the
familiar solution
(also obtainable with software),
's for which
(6.1) has nonzero solutions. Eq. (6.1)
is an elementary ordinary differential equation with the
familiar solution
(also obtainable with software),
X(x) := D1
cos( 1/2
x) + D2
sin(
1/2
x) + D2
sin( 1/2 x).
1/2 x).
Because of the boundary condition at x=0, we see that D1 = 0. We are left with
only one constant, which we can scale to 1, remembering that we may want to
multiply our solution by an arbitrary constant later. Because of the BC at
x=0, we now know that up to a constant multiple, X(x) =
sin( 1/2 x). The
other boundary condition in (6.2) tells us what the
allowable choices for
1/2 x). The
other boundary condition in (6.2) tells us what the
allowable choices for
 are, namely
are, namely
 1/2 = n
1/2 = n
 /L, n = 1,2,.... Taking L=1 for convenience,
the eigenfunctions and eigenvalues are:
/L, n = 1,2,.... Taking L=1 for convenience,
the eigenfunctions and eigenvalues are:
Xn(x) := sin(n
 x)
x)
 n := (n
n := (n
 )2
)2
Now let's look at the other part of the PDE which we "separated off":
T''(t) = -
 T(t)
(6.3)
T(t)
(6.3)
As we saw, there are many possible values of
 which are consistent with the
boundary condition for the function X, and the same possibilities occur in
equation (6.3) (multiply
which are consistent with the
boundary condition for the function X, and the same possibilities occur in
equation (6.3) (multiply
 by c2
here if c is not set to 1). Therefore
by c2
here if c is not set to 1). Therefore
Tn(t) = An cos(n
 t) + Bn sin(n
t) + Bn sin(n
 t).
t).
We cannot go further with the T function without being given the initial condition, that is, information about what happens at t=0.
We already have something of importance in science and engineering, however: the normal modes . Many physical systems, like the vibrating string, preferentially undergo simple motions with pure frequencies. Such a possible motion is exactly what we find by positing a product solution, imposing any boundary conditions, and solving the resulting eigenvalue problem.
Definition VI.1.
A
T(t) X(x),
where X(x) incorporates all boundary conditions.
Here the spatial variable x might be more than one-dimensional, as for the problem of the vibrating drum, which will be encountered
later. I have generalized the notion of a normal mode
so that any time dependence is allowed, although most commonly it will be
sinusoidal, T(t) = sin(
The general solution we come up with is a
linear combination of the particular
solutions we get by separating the equation. It is not yet obvious that this
is a completely general solution, but it is.
The coefficients A and B have to be determined from the initial conditions,
that is, by the condition of the string at t=0.
Suppose that
u(0,x) = f(x)
and
ut(0,x) = g(x)
(IC)
are given, and that 0 < x < 1. Plugging in to formula (6.4) shows that:
In other words, A[n] are the
Fourier sine coefficients for f(x),
and the more complicated expression
(n
gives the Fourier sine coefficients of g(x). Notice that the stuff in the sine
is n
but we can simplify this a bit by using the symmetry:
What about the other coefficients? Well, this time it is the whole expression
(n
Here is an example to illustrate the situation.
Model Problem VI.2. Solve the problem of the vibrating string using
Fourier sine series, and initial conditions
u(x,0) = 0, ut(x,0) = 1.
Solution.
We can easily calculate the formulae for the coefficients
A and B, either by hand or with software (see the Mathematica
notebook or Maple
worksheet):
Am = 0
If n is even, Bn = 0, else Bn = 4/(n
The general solution is
Next we show some plots of the solution at various times. For computational
purposes we keep terms only up to n=7.
In the
Mathematica
notebook or
Maple
worksheet you can see
the string vibrate by selecting the
graphs and choosing "animate."
By the way, infinity is larger than 7, but 7 is close enough to give us
a reasonable picture of the solution:
These are called Neumann boundary conditions. Obviously, as with DBC,
it would be a minor change to impose them
at x=a and x=b where a does not have to be 0. At this stage, we can exactly
repeat the analysis of separation of variables, until the point where we first
used the boundary conditions, i.e., (6.1). With NBC,
we instead evaluate the x-derivative at 0:
Model Problem VI.3. Set up the general solution of the vibrating string
with Neumann BC., with the simplifications c = L = 1.
Solution.
The partial differential equation separates exactly as before, so we still know
that when we assume u = X(x) T(t), we get separated equations (6.1) and (6.3).
The values of
X(x,
we see that
and for this to be 0 when x=0, there are two possibilities, namely
D1=0 or
Possibility 1.
(A0 + B0 t) 1 = A0 + B0 t.
Since the boundary conditions do not apply to the t variable, we keep the
general
linear combination.
A0 and B0 will be determined by the initial
conditions.
Possibility 2.
(An cos(n
and the general solution will be
The coefficients are determined by the initial conditions because:
The numbers An are the Fourier cosine coefficients of u[(0,x) = f(x), while
B0 and n
utt = (c(x))2 uxx
(ModWE1)
or, as a thorough examination of the derivation of the wave equation
reveals,we could more generally have:
for some potentially complicated positive functions p(x) and s(x). How well does
the method of separation of variables do for problems like this? Rather well,
actually, although we may have to encounter some new functions.
Model Problem VI.4. Suppose that the wave speed depends on position, so that
Find the normal modes of vibration.
Exercises VI
f(x) = |x-1/2|, g(x) = x2
Do you encounter any difficulties because the IC are not consistent with the
BC?
f(x) = sin(
a) DBC at x=0 and x=1
Plot the solutions and compare.
f(x) = 0, g(x) = 1
and
a) DBC at x=0 and x=1
Plot the solutions and compare.
f(x) = sin(
a) DBC at x=0 and x=1
Plot the solutions and compare.
and
Dirichlet boundary conditions at x=0 and x=
utt + u = uxx
with Neumann boundary conditions:
ux(t,0) = 0
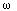 t +
t +
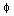 ). When it is sinusoidal, the angular
frequency omega is usually a simple function of the eigenvalue.
). When it is sinusoidal, the angular
frequency omega is usually a simple function of the eigenvalue.
(6.4)
 ) Bn
) Bn  x/L and not
x/L and not
2 n
 x/L (with L=1). In other words, there are more
sines in this series than in the usual Fourier series, but there are no
cosines. It is precisely as if we imagine the string to be defined on the
interval [-1,1], twice as long as the actual interval, but on the nonphysical
part from x=-1 to x=0 we pretend that the shape of the string is defined to
give us an odd function: f(-x) = -f(x). This would give us only sine
functions, as we have seen before. Earlier we called those coefficients
Bn, but here they happen to be called An.
The thing to remember is that since
they go along with sine functions (of x) the formula for them contains sines. We
would thus write
x/L (with L=1). In other words, there are more
sines in this series than in the usual Fourier series, but there are no
cosines. It is precisely as if we imagine the string to be defined on the
interval [-1,1], twice as long as the actual interval, but on the nonphysical
part from x=-1 to x=0 we pretend that the shape of the string is defined to
give us an odd function: f(-x) = -f(x). This would give us only sine
functions, as we have seen before. Earlier we called those coefficients
Bn, but here they happen to be called An.
The thing to remember is that since
they go along with sine functions (of x) the formula for them contains sines. We
would thus write
 ) Bn
which is a Fourier sine coefficient
for g(x), so we need to divide
through by the extra factor:
) Bn
which is a Fourier sine coefficient
for g(x), so we need to divide
through by the extra factor:
and
 )2
)2
The boundary conditions we have been using are not the only useful ones.
Suppose that our string is attached to a pair of tracks in the vertical
direction perpendicular to the x-axis using a frictionless roller.
Then u(t,0) and u(t,L) are not specified,
but instead we have:
(NBC)
 will be different, however, because they were determined by the
BC. Since as before,
will be different, however, because they were determined by the
BC. Since as before,
 ) := D1
cos(
) := D1
cos( 1/2
x) + D2
sin(
1/2
x) + D2
sin( 1/2 x),
1/2 x),
 =0.
(We ignored the latter possibility before since sin(0) = 0 is not a useful
solution, but cos(0) = 1 can be one.)
=0.
(We ignored the latter possibility before since sin(0) = 0 is not a useful
solution, but cos(0) = 1 can be one.) =0, which means that the output just given is not really the
solution to (6.1), which has become X''(x) = 0. The solutions of this are of
the form A + B x, but B has to be 0 so that X'(0) = 0. Thus with this
possibility, X(x) = 1 (times any constant). Eq. (6.3) now also becomes T''(t)
= 0, which leads to the product solution of (WE):
=0, which means that the output just given is not really the
solution to (6.1), which has become X''(x) = 0. The solutions of this are of
the form A + B x, but B has to be 0 so that X'(0) = 0. Thus with this
possibility, X(x) = 1 (times any constant). Eq. (6.3) now also becomes T''(t)
= 0, which leads to the product solution of (WE): > 0. The boundary condition at x=0 now forces
X(x) = cos(
> 0. The boundary condition at x=0 now forces
X(x) = cos(
 1/2 x) (again, up to a constant multiple),
and the other boundary
condition forces one of the values
1/2 x) (again, up to a constant multiple),
and the other boundary
condition forces one of the values
 n = (n
n = (n
 )2.
The product solutions become
)2.
The product solutions become t) + Bn sin(n
t) + Bn sin(n
 t)) cos(n
t)) cos(n
 t)
t)
(6.5)
and
 Bn are the Fourier cosine coefficients of
ut(0,x) = g(x).
(Notice the extra factors of n
Bn are the Fourier cosine coefficients of
ut(0,x) = g(x).
(Notice the extra factors of n  .)
.)
A realistic string or optical fiber may not be uniform, so some of the
simplifying
assumptions in our derivation fo the wave equation are not valid. For example,
the
constant c2 = (spring constant) / (mass density) for the spring may be different
at different
positions, leading to an equation of the form
(ModWE2)
c2 = 1/(1 + x), 0 < x < 1, DBC at 0 and 1.
Solution.
 x), g(x) = 0
and
x), g(x) = 0
and
b) NBC at x=0 and x=1
c) DBC at x=0 and NBC at x=1
b) NBC at x=0 and x=1
c) DBC at x=0 and NBC at x=1 x), g(x) = 1
and
x), g(x) = 1
and
b) NBC at x=0 and x=1
c) DBC at x=0 and NBC at x=1
 , 0 < t <
, 0 < t <
 ,
initial conditions:
,
initial conditions:
 , i.e., u(t,0) = u(t,
, i.e., u(t,0) = u(t,
 ) = 0,
for 0 < t.
) = 0,
for 0 < t.
ux(t,
 ) = 0
) = 0
where g, the gravitational constant, is approximately 980 in the cgs system.
u(t, 0) = u(t, L) = 0, and
uxx(t, 0) = uxx(t,L) = 0.
Link to