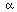 v+
v+ 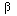 w,
w,
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
Theorem II.3. If V is an inner product space, then the CSB inequality (Property 5) and the triangle inequality (Property 6) hold.
proof (don't worry -it won't hurt you!): Because of the positivity property 4,
the square length of any vector is >= 0, in particular for any linear
combination 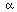 v+
v+ 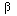 w,
w,

The trick now is to choose the scalars just right. Some clever person - perhaps
Hermann Amandus Schwarz - figured out to choose 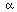 = ||w||2 and
= ||w||2 and
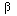 = - <v,w>. The
inequality then boils down to
= - <v,w>. The
inequality then boils down to
0 <= ||w||4 ||v||2 - ||w||2 |<v,w>|2.
If we collect terms and divide through by ||w||2, we get the CSB inequality. (If ||w||=0, the CSB inequality is automatic; otherwise we can divide it out.)
For the triangle inequality, we just calculate:
||v+w||2 = <v+w,v+w> = <v,v> + <w,w> + 2 Re(<v,w>) <= ||v||2 + ||w||2 + 2 ||v|| ||w|| <= (||v|| + ||w||)2 .QED
Return to chapter II
Return to Table of Contents
Return to Evans Harrell's home page