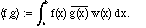 Another is to make the functions and integrals multidimensional, running over
some region
Another is to make the functions and integrals multidimensional, running over
some region
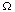 :
:
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
Examples II.2, continued.
4. Other inner products for functions. We can generalize
Example 3 in various ways. The first is to insert a
positive weight function w(x):
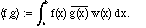 Another is to make the functions and integrals multidimensional, running over
some region
Another is to make the functions and integrals multidimensional, running over
some region
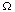 :
:
5. An inner product for matrices considered as vectors.
Let the vector space V be the set of mxn matrices. Define the
adjoint M* of a matrix M with entries mjk to be the nxm matrix the
entries of which are
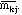 Define the trace of a matrix by
Define the trace of a matrix by
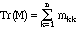 (sum the diagonal elements). Then
(sum the diagonal elements). Then
<M,N> := Tr(M N*) is an inner product.

Or - here is a really great one - we could have weight functions and lots of dimensions! Yeah.....
Link to