Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
*(c) Copyright 1994-2000 by Evans M. Harrell
II and James V. Herod. All rights reserved.
version of 12 January 2000
Green functions in Rn.
BEING REVISED!
The printed version of these notes is an appendix to the rest. In this Web version,
it consists of links bringing out the analogies between integral operators and
matrices.
The common setting for the two subjects is an
inner product space, which was defined abstractly in the
chapter entitled
The Geometry of Functions.
Since the idea of
an inner product, or dot product, arises in such a variety of problems, we
should recall exactly what are the properties that define an inner product and
what are some of the consequences of these properties.
Appendix A1 ARITHMETIC AND GEOMETRY IN Rn
If E is the linear space on which the inner product is defined and x and y are
in E, then < x, y > denotes the (perhaps, complex) number which is the
inner product of x and y. it has several useful and important peoperties:
1. The inner product is a mapping taking pairs of vectors and producing
scalars
2. Linearity :
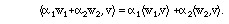
Note: some texts define an inner product to be linear on the right side rather
than the left side. This makes no practical difference, but if there are
complex quantities, you should be careful to be consistent with whichever
convention you follow.
3. Symmetry :

(The bar denotes complex conjugate, in case these are complex numbers.)
4. Positivity :

5. The Cauchy,
Schwarz, or
Buniakovskii inequality
(depending on your nationality):
 (2.3)
(2.3)
6. The triangle inequality :
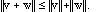 (2.4)
(2.4)
We need Property 5 if an inner product is to correlate with Eq. (2.1), and we
need Property 6 if the norm (=length)
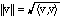
is to make sense geometrically.
EXAMPLE: One can think of a weighted dot product on
Rn by choosing a positive number sequence ap, p=1...n
and defining < x, y > to be given by
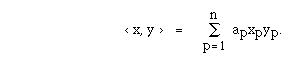
The usual inner product on Rn is the one obtained in the
above example by choosing ap = 1 for p= 1...n.
In this setting, we can
think of the structure of Rn in the language of Euclidean geometry:
the distance between x and y is ||x-y|| and the angle between x and y is
 , where
, where
0



 and
and

provided neither x nor y is zero. For example, points x and y are
perpendicular, or orthogonal, if < x, y
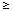 0. Also, the concept of
distance provides a notion of points being "close together". It is natural to
say that the sequence {vp} of points in Rn has limit the point y in
Rn provided
0. Also, the concept of
distance provides a notion of points being "close together". It is natural to
say that the sequence {vp} of points in Rn has limit the point y in
Rn provided
limp || vp - y || = 0.
It is of value, even at this elementary level, to realize that there are
several ways to think of the idea "limp vp = y". In Rn, the
following three are equivalent:
The sequence {vp} in Rn converges to y component wise if for
each integer i, 1  i
i
 n,
n,
limp(vp)i = yi.
The sequence {vp} in Rn converges to y uniformly if
limp( maxi | xp(i) -y(i) | )= 0.
The sequence {vp} in Rn converges to y in norm if
limp||vp - y|| =0.
It is not difficult to establish that these three notions are equivalent
in Rn. The value of thinking of them separately here is that the
three methods of convergence have analogues in situations which we will
encounter in later sections. In those situations, the three methods of
convergence may be not equivalent.
Fundamental in the development of Green's Functions will be
the
Riesz
Representation Theorem: If L is a linear function from Rn to R then
there is a vector v in Rn such that L(u) = < u, v
> for all u in Rn. Closely related to the Riesz
Representation Theorem is the fact that every linear function from
Rn to Rn has a matrix representation. These ideas are
familiar.
Appendix A2:
THE ADJOINT A*
Linear functions and matrices arise in many ways. Here is one that
you might not have considered. Choose an nxn matrix A. Consider all points x
and y in Rn related by
< Au, x > = < u, y >
for all u in Rn. To be sure that, given x, there is such a point y,
consider the following: pick x; then L(u) = <Au, x > is a linear
function of u from Rn to R. By the Riesz Representation Theorem,
there is a point y in Rn such that L(u) = < u, y > for all u
in Rn. Define this y as B(x). It can be established that B is,
itself, a linear function from Rn to Rn. Hence, it has a
matrix representation. This linear function B is called the adjoint of A and is
denoted as A*. For all x and u in Rn,
< Au, x > = < u, A*x >.
The concern of this course, stated in the context of Rn, is the
following problem: given a matrix A and a vector f = {f1 ,f2 , ...fn}, can a
vector u be found such that Au = f? There are matrices A and vectors f such
that the equation Au=f has exactly one solution, or no solution, or an infinity
of solutions.
Appendix A3 THE
FREDHOLM
ALTERNATIVE THEOREMS
The following ideas will persist in each segment of the course. These
fundamental results are known as the Fredholm Alternative Theorems. For
matrices, the alternatives hinge on whether or not the determinant of A is zero
or not.
I. Exactly one of the following two alternatives holds:
(a)(First Alternative) if f is in Rn, then Au = f has
one and only one solution.
(b)(Second Alternative) Au= 0 has a nontrivial solution.
II. (a) If the first alternative holds for A, then it also holds for A*.
(b) In either alternative, the equations Au= 0 and A* u = 0 have the
same number of linearly independent solutions.
III. Suppose the second alternative holds. Then Au=f has a solution if and
only if < f, z > = 0 for each z such that A*z=0.
A matrix problem is well- posed if
(a) for each f, the equation Au=f has a solution,
(b) the solution is unique, and
(c) the solution depends continuously on the data-- in the sense that if f is
close to g and u and v satisfy Au=f and Av = g, then u is close to v.
Appendix A4 SOLVING EQUATIONS
Just as there are many ways to conceive of solving Au=f in case A is a
matrix, so there are many ways for finding solutions for problems which are
introduced in the next chapters. We concentrate on the method of constructing
a Green's function. From what has come before, it may be clear that in some
sense, we are finding an inverse for the linear operation A.
THE FIRST ALTERNATIVE
We discuss the solution of the linear equation
Au = f,
where we suppose we are given a matrix A and know f. Don't be to quick to
dismiss the solution as u = A-1 f. While that is correct, we want
perspective here, not just results.
Here is an adaptation of the methods which we will use to find Green's
functions in two chapters from here: Let deltai be the vector which has the
property that
< deltai, u > = u(i)
for all u in Rn. One can write the components for deltai
deltai = {0,0,...0. 1, 0, ... 0}
where the 1 is in the i-th component. Note that
u = [[Sigma]]i deltai u(i).
Let A be an nxn matrix and f be a vector. In order to solve Au=f, we seek
G(i,j) such that u defined by
< G(j,.) , f(.) > = u(j)
(*)
might provide the solution for Au=f.
Look again at equation (*). Writing the dot product as a sum changes that
equation to

or, in the notation of matrix multiplication,
Gf = u.
In what follows, perhaps you will see that writing the equation as (*) or (**)
provides unifying ideas.
Here is a proposal for how humans find G. Find G such that
A(G( ,i))= deltai.
That is, A(G( ,i))(m) = deltai(m).
Having such a G, define u by
u(j) = [[Sigma]] i G(j,i)f(i).
Then
[A(u)](m) = [[Sigma]]j A(m,j) u(j) = [[Sigma]] j A(m,j) [[Sigma]] i
G(j,i)f(i)
= [[Sigma]] i [[Sigma]] j A(m,j)G(j,i)f(i)
= [[Sigma]] ideltai(m) f(i) = f(m).
This is what was desired: u solves the equation
Au = f.
Here is an alternate approach to the problem: Consider these relations:
<deltai,u> = u(i) = <G(i,.),f(.)> = <G(i,.),Au> =
<A*G(i,.),u>.
Thus, we might seek G such that deltai = A*G(i,.). Go back and re-do the above
exercise this way to see if you get the same answer. Here's a proof that you
should fill in with details.
THEOREM. Suppose that A and G are matrices. These are equivalent:
(a) A(G( ,i)) = deltai and (b) A*(G(i, )) = deltai.
Suggestion for a proof. Let G1 be defined by the first equation:
A(G1( ,i)) = deltai
and G2 be defined by the second equation:
A*(G2(i, )) = deltai.
Then G1(j,i) = < dj , G1( ,i) > = < A*(G2(j, )) , G1( ,i))
>
= < G2(j, ) , A(G1( ,i)) > = < G2(j, ) , deltai
> = G2(j,i).
THE
SECOND ALTERNATIVE
In case the determinant of A is zero and we are in the second
alternative, we can still conceive of the possibility of constructing G such
that if f is perpendicular to the null space of the adjoint of A, then
u(j) = < G(j, ), f >
provides a solution to the equation Au = f. The methods developed above will
not work for, given i, we cannot find a vector G(i, ) that solves A(G(i, )) =
deltai. To see this, recall the third part of the Fredholm Alternative Theorem and
then note that
< deltai,v >
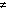 0
0
for all vectors v in the nullspace of A*. Thus, in this second alternative, we
must modify the method.
Let
 be a maximal orthonormal sequence in the nullspace of A*. We know there is G(
,p) in Rn such that
be a maximal orthonormal sequence in the nullspace of A*. We know there is G(
,p) in Rn such that

for < dp- [[Sigma]]i=1vi( ) vi(p) , w > = 0
for all w in the nullspace of A*. We will show that u(i) defined by
< G(i, ), f >
satisfies the equation Au = f. In fact,
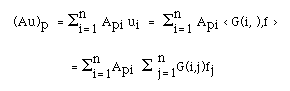

Exercises
A.1.
(a) Suppose that L: R3 -> R and is defined
by L(u) = 2u1-u3. Find v such that L(u) = < u, v > for all
u on R3.
(b) Suppose that L: R3 -> R and is defined by L(u)= u2.
Find v such that L(u) = < u, v >.
(c) Give the matrix representation of L: R3 -> R3
if L(u) = {3u1+2u3, -u1+u2, u1-u2+u3}.
A.2.
(a)

(b) For the following matrices A and vectors f, determing whether the equation
Au = f has exactly one solution, no solution or an infinity of solutions. If
there are solutions, find them.


A.3.
(a) For each of the matrices listed below determine what
is the dimension of the null space of A and of the null space of A*? Give a
basis for each. Find one f such that < f, z > = 0 for each z in the null
space of A*. Solve Au = f. Find g such that < g, z >
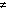 0 for each z
in the null space of A*. Show that one can not solve Au=g for this g.
0 for each z
in the null space of A*. Show that one can not solve Au=g for this g.

(b) Let

Show that the problem A1 u = f is well posed and the problem
A2 u = f is not.
A.4.
(a) For the following matrices A, show that det(A) = 0, Find an orthonormal
basis for the null space of A*. Make up G. For the given f show that is it is
perpendicular to the null space of A*. Show that u as defined by equation (*)
in the discussion of the First Alternative solves Au=f.


(2) Take

Find G such that the equation
< G(i .), f(.) > = u(i)
provides a solution for Au = f for any vector f. ( Be aware that high school
students know how to do this without ever thinking of the vector deltai!)
Link to
chapter IV
chapter II
Table of Contents
Evans Harrell's home page
Jim Herod's home page
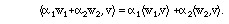


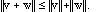 (2.4)
(2.4)

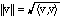
 , where
, where

 and
and 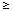 0. Also, the concept of
distance provides a notion of points being "close together". It is natural to
say that the sequence {vp} of points in Rn has limit the point y in
Rn provided
0. Also, the concept of
distance provides a notion of points being "close together". It is natural to
say that the sequence {vp} of points in Rn has limit the point y in
Rn provided
 0
0