Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 14 March 2000
Here is a Mathematica notebook with calculations for this chapter, and here are some Maple worksheets with similar calculations
In this chapter we shall learn how to solve integral equations in three situations:
Definition XIV.1 Suppose that there are an integer n and functions
such that, for each p , ap and bp are in
L2[0,1]. Then K has
a
separable kernel if its kernel is given by
Another term for operators K of this type is finite-rank, and we shall
see that they can be considered as matrices of finite rank.
With the supposition that K is separable, it is not hard to find y such
that y = Ky + f, for this equation can be re-written as
or, using the notation of inner products,
We can see that if the sequence
there is a sequence {cp} of numbers such that
Why is this? In (14.1), all the definite integrals
over t are just numbers. Even though we do not know their values yet,
we can call them cp and procede to determine their values
with a bit of algebraic labor.
Suppose
Substitute this in the equation to be solved:
and we see that
This now reduces to a matrix problem:
Define K and f to be the matrix and vector so defined that the
last equation is rewritten as
c = K c
+ f.
We now employ ideas from linear algebra. The equation c
= K c +
f has exactly one solution provided
(14.1)
(14.2)
(14.3)
of
functions on [0,1] is a linearly independent sequence, then y will have
the following
special form:
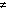 0.
0.
is found, we have a formula for y(x).
Example XIV.2: In the exercises of chapter XIII, it should have been established that if
K(x,t) = 1 + sin( x) cos(
x) cos( t),
t),
then
K*(x,t) = 1 + sin( t) cos(
t) cos( x).
x).
Also,
y = Ky has solution y(x) = 1
and
y = K*y has solution y(x) =  + 2 cos(
+ 2 cos( x).
x).
It is the promise of the Fredholm Alternative theorems that
y = Ky + f
has a solution provided that
Let us try to solve y = Ky + f and watch to see where the requirement
that f should be perpendicular to the function  +2 cos(
+2 cos( t)
appears.
t)
appears.
To solve y = Ky + f is to solve
As usual we see that the solution
must be of the form y(x) =
a + b sin( x) + f(x),
and
substitute this for y:
x) + f(x),
and
substitute this for y:
From this, we get the algebraic equations
Hence, in our guess for y, we find that a can be anything and that b must be
and b must also be
The naive pupil might think this means there are two (possibily contradictory) requirements on b. The third of the Fredholm Alternative theorems assures the student that there is only one requirement!
Take  0(x) to be f(x) and
0(x) to be f(x) and  1 to be defined by
1 to be defined by
It is reasonable to ask: does this generated sequence converge to a limit and in what sense does it converge? The answer to both questions can be found under appropriate hypothesis on K.
Theorem XIV.3. If
K satisfies the condition that
then limp
limp maxx | u(x) -
Proof. Note that
Furthermore, if p is a positive integer, the distance between successive
iterates can be computed:
Inductively, this does not exceed
Thus, if
and n > m then
Hence, the sequence {
Corollary XIV.4. If
and
u = limp
then
Sometimes it is convenient to express the iteration as an infinite
series, called the Neumann series, i.e., the sum of
Model Problem XIV.5.
Consider the integral equation
where g(x) is given. We wish to solve for u(x), and we try the
method of iteration.
We begin with the guess
This integral can be simplified by reversing the order of integration.
Setting the limits takes a moment of reflection, and may be helped
by the following diagram:
The relationship of the variables is 0 < t < t1 < x. If the first
(inside) integral is in the variable t, then it runs from 0 to
t1, and then the
second integral in the variable t1 runs from 0 to x.
If we reverse the
order, the first integral, in the variable t1,
runs from t to x, and
the second integral runs from 0 to x. We find that
If we now calculate the further iterates, we find inductively that
It is a miracle when the series for K sums in
closed form like this, but that is not important in applications,
since the convergence of the Neumann series implies that we can calculate
the answer to any desired accuracy.
Theorem XIV.6. If K satisfies the
Hilbert-
Schmidt condition (14.4),
then limp
limp || u(x) -
INDICATION OF PROOF. The analysis of the nature of the convergence will go
like this:
As a consequence, the sequence
Let's state the conclusion in a careful way:
Corollary XIV.7. If
Then
Before addressing the final case - where
Re-examining the iteration process:
One writes
In fact, with
Hence, the kernel K2 associated with K2 is
Inductively,
and
We have, in this section, conditions which imply that
Link to
(14.4)
 p(x) exists and the convergence is
uniform on [0,1] - in the
sense that if u = limp
p(x) exists and the convergence is
uniform on [0,1] - in the
sense that if u = limp p then
p then p(x) | = 0.
p(x) | = 0.  p} of functions converges uniformly on [0,1] to a
limit function and this limit provides a solution to the equation
p} of functions converges uniformly on [0,1] to a
limit function and this limit provides a solution to the equation p
p  n =
n =
 n-
n- n-1.
We reason this way in the next example.
n-1.
We reason this way in the next example.
 0 = g(x), and calculate the
next couple of iterates:
0 = g(x), and calculate the
next couple of iterates:
 2(x) is:
2(x) is:
There is different, independent, way in which
K can be considered small, which leads
to convergence of the iteration process in the
norm of L2[0,1].
This
hypothesis asks that
(14.5)
 p(x)
exists and the convergence is in the
r.m.s. sense, that is:
p(x)
exists and the convergence is in the
r.m.s. sense, that is:
 p(x) || = 0.
p(x) || = 0.
 1 -
1 -
 2|| 2
2|| 2
 n
is Cauchy convergent:
n
is Cauchy convergent:
,
 p
p
Definition The
resolvent of an operator K is the inverse operator
(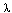 - K)-1.
This is same as the solution operator for the
equation
- K)-1.
This is same as the solution operator for the
equation
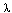 Ky + f
Ky + f
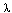 is taken as 1, and unless stated
otherwise we shall always do this.
is taken as 1, and unless stated
otherwise we shall always do this.
 0(x) = f(x),
0(x) = f(x), 1(x) = K
1(x) = K 0(x) + f(x)
0(x) + f(x) 2(x) = K(K(
2(x) = K(K( 0))x +
K(f)(x) + f(x)
0))x +
K(f)(x) + f(x)
 0=f,
0=f,  1=Kf+f,
1=Kf+f,  2 =
K[Kf+f] + f = K2f+Kf+f, .....
2 =
K[Kf+f] + f = K2f+Kf+f, .....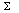 p=1
Kpf
p=1
Kpf
R = 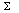 p=1 Kp.
(14.6)
p=1 Kp.
(14.6)