Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
*(c) Copyright 2000
by Evans M. Harrell
II and James V. Herod. All rights reserved.
version of 5 April 2000
(Some remarks for the instructor).
Green functions, Fourier series, and eigenfunctions.
In this chapter we shall discuss a method for finding Green functions which
makes little reference to whether a linear operator comes from an
ordinary differential equation, a partial differential equation,
or some other, abstract context.
In
Chapter XVI we used some special
one-dimensional features in order to find Green functions of
ordinary differential equations. Hence we begin by reviewing which
of the facts we used were connected with the one-dimensional
nature of the independent variable x. We do this in tabular form.
Facts about Green Functions and Differential Equations
which are Independent of Dimensionality
-
The Green function is the integral kernel of a linear operator which
inverts a differential operator L
-
The Green function solves (weakly) a differential equation
of the form
Lx G(x,t) =
 (x,t)
including the boundary conditions which accompany the differential equation
L y = f
(x,t)
including the boundary conditions which accompany the differential equation
L y = f
-
Any two Green functions for the same differential equation
(say, with different boundary conditions)
have a difference which satisfies the
homogeneous equation L y = 0.
On the other hand, at several points we relied on facts which,
unfortunately, just won't be available for partial differential
equations:
Facts about Green Functions and ODEs
which are Strictly One-Dimensional
-
The dimension of the null space of an ordinary differential operator
of order n is n.
-
The solutions of a homogeneous linear ordinary differential equation
satisfy a Wronskian identity.
-
The solutions to a well-posed initial-value problem for an ordinary
differential equation exist and are unique. (With the method of
characteristics there is an analogy for partial differential equations,
but it is substantially more complicated.)
-
The
 function can be regarded as the derivative of a step function.
function can be regarded as the derivative of a step function.
- The Green function satisfies a
"jump condition" at x=t.
In this chapter our method will use
infinite series to construct Green functions. It will require some
special assumptions, but those can often be guaranteed
whether the independent variable x is one dimensional
or many dimensional.
The important assumption will be that
the linear operator L has a
complete set of orthogonal eigenfunctions. Here
completeness is meant in the sense of
Chapter III. That is, we assume that
there is a linear operator L such that the set of eigenvectors ek:
L ek = 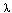 k ek
where <ej, ek>=0 for
j
k ek
where <ej, ek>=0 for
j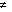 k, and
where any vector f in the Hilbert space can be written as
k, and
where any vector f in the Hilbert space can be written as
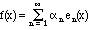 .
(17.1)
We shall soon recall some situations where the assumptions are justified for
differential operators, whether in one dimension or in many
dimensions,
but let us first discuss the general set-up, where
we are trying to solve an equation of the form
L u = f
If we write
.
(17.1)
We shall soon recall some situations where the assumptions are justified for
differential operators, whether in one dimension or in many
dimensions,
but let us first discuss the general set-up, where
we are trying to solve an equation of the form
L u = f
If we write
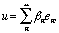 (17.2)
and act on both sides with the operator L, then (putting aside the question
of interchanging the order of the sum and the linear operator), we find:
(17.2)
and act on both sides with the operator L, then (putting aside the question
of interchanging the order of the sum and the linear operator), we find:
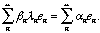 Clearly, if none of the eigenvalues are 0 and there are no problems with
convergence, we can solve for the
Clearly, if none of the eigenvalues are 0 and there are no problems with
convergence, we can solve for the 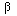 n
n
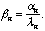 Because the eigenvectors en are orthogonal, we have a
formula for the
Because the eigenvectors en are orthogonal, we have a
formula for the 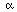 n
as in
Chapter III:
n
as in
Chapter III:
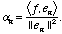 If we refer again to (17.2), we get a formula for the inverse operator:
If we refer again to (17.2), we get a formula for the inverse operator:
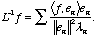 (17.3)
To this stage, everything is abstract. Now, let us assume that the eigenvectors
are eigenfunctions, so that the inner product becomes an integral.
We find:
(17.3)
To this stage, everything is abstract. Now, let us assume that the eigenvectors
are eigenfunctions, so that the inner product becomes an integral.
We find:
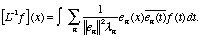 The infinite sum in this expression is the kernel of an integral operator
which solves L u = f - it must be the Green function!
The infinite sum in this expression is the kernel of an integral operator
which solves L u = f - it must be the Green function!
Model Problem XVII.1. Let us use this method to solve the boundary-value
problem
-u'' + u = f, u(0) = u(1) = 0.
(17.4)
Solution.
We first ask for non-zero solutions ek(x) of the
eigenvalue problem:
(-D2 + I) ek(x) =
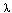 k ek(x)
k ek(x)
Boundary conditions: ek(0) = 0 = ek(1) = 0.
(17.5)
The solutions of the differential equation (17.5) are combinations of
sin(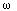 x) and
cos(
x) and
cos(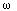 x). The boundary condition
ek(0) = 0 eliminates the cosines, and the other condition
severely limits the possibilities for
x). The boundary condition
ek(0) = 0 eliminates the cosines, and the other condition
severely limits the possibilities for
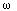 , and therefore for
, and therefore for
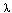 k:
(-D2 + I) sin(k
k:
(-D2 + I) sin(k  x)
= (k2
x)
= (k2
 2
+ 1) sin(k
2
+ 1) sin(k  x).
As we know from
Chapter VI, these sine functions are a
complete orthogonal set. That is, any square-integrable function
F(x) can be written as a
Fourier sine series in terms of these functions.
x).
As we know from
Chapter VI, these sine functions are a
complete orthogonal set. That is, any square-integrable function
F(x) can be written as a
Fourier sine series in terms of these functions.
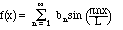 According to the ideas of this chapter, the solution of
(17.4) is
According to the ideas of this chapter, the solution of
(17.4) is
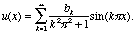 (17.6)
(17.6)
Because of the
formula for the coefficients bk,
we see that the
Green function is:
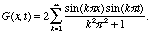 (17.7)
(17.7)
As mentioned, this method makes little reference to the fact that
the L of Model Problem XVII.1 is an ordinary differential operator.
Let us consider the same problem from a different point of view, by
expanding the delta function in a
Fourier sine series.
Bravely applying the
usual formulae
for the Fourier sine series to the delta function, we find that
for 0 < x < 1,
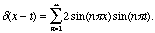 In other words, if the function f(x) above happens to be
the delta function, then
bn =
2 sin(n
In other words, if the function f(x) above happens to be
the delta function, then
bn =
2 sin(n t).
If we now use (17.6), we get the same formula (17.7) for the
Green function.
t).
If we now use (17.6), we get the same formula (17.7) for the
Green function.
Let us now turn our attention to some partial differential equations
which use the
Laplace operator, introduced in
Chapter IX. We begin with
Laplace's equation (9.1-2):
Model Problem XVII.2. Let us use the same method to solve
the two-dimensional boundary-value
problem for 0 < x1, x2 < 1,
- 2
u = f(x),
(17.8)
2
u = f(x),
(17.8)
Boundary conditions: u = 0 when either x1 = 0 or 1
or x2 = 0 or 1.
Solution.
We can solve this problem with a
double
Fourier sine series. The reason for this is that
the sine functions
fjk(x) :=
sin(j  x1)
sin(k
x1)
sin(k  x2)
are not only a
complete set,
but also have a special relationship to the Laplace operator, as
eigenfunctions (including the correct boundary conditions):
x2)
are not only a
complete set,
but also have a special relationship to the Laplace operator, as
eigenfunctions (including the correct boundary conditions):
- 2
fjk(x) =
2
fjk(x) =
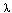 jk fjk(x),
where
jk fjk(x),
where
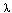 jk :=
(j2 + k2)
jk :=
(j2 + k2)
 .
As remarked above, we may derive the series for the Green function by
treating it as a classical function and finding its Fourier series
by exploiting the equation
(17.8)
with f(x) =
.
As remarked above, we may derive the series for the Green function by
treating it as a classical function and finding its Fourier series
by exploiting the equation
(17.8)
with f(x) =
 (x-
(x-
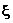 )
for any given vector
)
for any given vector
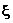 .
.
Since
 (n)(x
-
(n)(x
-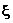 ) =
) =
 (x1-
(x1-
 1)
1)
 (x2-
(x2-
 2)
(see the Exercises), The Fourier series for
the two-dimensional delta function is likewise a product:
2)
(see the Exercises), The Fourier series for
the two-dimensional delta function is likewise a product:
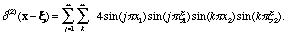 At the same time, if
At the same time, if
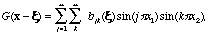 then
then
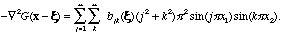 By comparing these equations, we determine the coefficients
By comparing these equations, we determine the coefficients
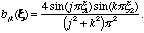
Exercises XVII
-
In Exercises 5, 13, 14, and 19 of
Chapter 16, you constructed Green functions for
different boundary conditions but the same differential equation of
the form LxG = f. Verify
in each such case that
if you define y := G(a)(x,t) - G(b)(x,t),
then y solves the homogeneous differential equation Lxy = 0.
-
The
Green function of Model Problem XVII.1
must be the same as the one you found in
Exercise 10 (d) of
Chapter XVI, despite looking entirely different. Show that the two
Green functions are equal.
-
Using the
definition of the delta function, show
that if
 (n)(x
-
(n)(x
-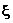 ) denotes the delta
function in n dimensions, then
) denotes the delta
function in n dimensions, then
 (n)(x
-
(n)(x
-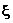 ) =
) =
 (x1-
(x1-
 1)
1)
 (x2-
(x2-
 2)...
2)...
 (xn-
(xn-
 n).
n).
-
Use the
Fourier cosine series to find the Green function
for the boundary-value problem
-
 2
u + u = f(x),
(17.9)
2
u + u = f(x),
(17.9)
Boundary conditions of Neumann type:
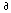 u/
u/
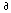 x1 = 0 when x1 = 0 or 1, and
x1 = 0 when x1 = 0 or 1, and
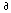 u/
u/
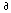 x2 = 0 when x2 =
0 or 1.
Note: The addition of u in (17.9) prevents the problem from being in the
second Fredholm alternative. SHow that
if combine the Neumann boundary conditions of this problem with the
equation in
(17.8), then the second alternative applies.
x2 = 0 when x2 =
0 or 1.
Note: The addition of u in (17.9) prevents the problem from being in the
second Fredholm alternative. SHow that
if combine the Neumann boundary conditions of this problem with the
equation in
(17.8), then the second alternative applies.
-
Solve the Poisson equation
(17.8)
on the rectangle 0 < x1 < 2, 0 < x2 < 1,
with Dirichlet (u=0) boundary conditions on the boundary.
-
Solve the Poisson equation
(17.8)
on the rectangle 0 < x1 < 2, 0 < x2 < 1,
with Dirichlet (u=0) boundary conditions at x1 = 0 and 2, but
Neumann boundary conditions at x2 = 0 and 1.
-
Solve the Poisson equation
(17.8)
on the rectangle 0 < x1 < 2, 0 < x2 < 1,
with Dirichlet (u=0) boundary conditions at x1 = 0 and
x2 = 0, but
Neumann boundary conditions at x1 = 2 and x2 = 1.
Note: First figure out what the eigenfunctions are which satisfy the
boundary conditions. The spectral theorem guarantees that they are
a complete orthogonal set.
Link to
chapter XVIII
chapter XVI
Table of Contents
Evans Harrell's home page
Jim Herod's home page
 (x,t)
(x,t)
 (x,t)
(x,t)
 function can be regarded as the derivative of a step function.
function can be regarded as the derivative of a step function.
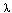 k ek
k ek
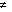 k, and
where any vector f in the Hilbert space can be written as
k, and
where any vector f in the Hilbert space can be written as
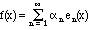 .
(17.1)
.
(17.1)
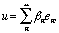 (17.2)
(17.2)
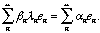
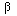 n
n
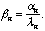
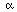 n
as in
Chapter III:
n
as in
Chapter III:
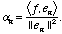
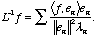 (17.3)
(17.3)
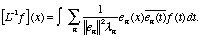
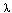 k ek(x)
k ek(x)
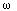 x) and
cos(
x) and
cos(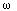 x). The boundary condition
ek(0) = 0 eliminates the cosines, and the other condition
severely limits the possibilities for
x). The boundary condition
ek(0) = 0 eliminates the cosines, and the other condition
severely limits the possibilities for
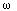 , and therefore for
, and therefore for
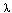 k:
k:
 x)
= (k2
x)
= (k2
 2
+ 1) sin(k
2
+ 1) sin(k  x).
x).
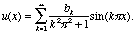 (17.6)
(17.6)
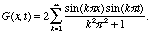 (17.7)
(17.7)
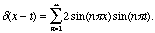
 t).
t).
 2
u = f(x),
(17.8)
2
u = f(x),
(17.8)
 x1)
sin(k
x1)
sin(k  x2)
x2)
 2
fjk(x) =
2
fjk(x) =
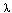 jk fjk(x),
jk fjk(x),
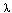 jk :=
(j2 + k2)
jk :=
(j2 + k2)
 .
.
 (
(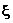 )
for any given vector
)
for any given vector
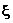 .
.
 (n)(x
-
(n)(x
-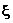 ) =
) =
 (x1-
(x1-
 1)
1)
 (x2-
(x2-
 2)
2)
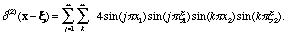
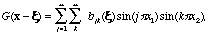
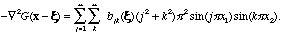
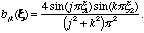
 (n)(x
-
(n)(x
-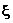 ) denotes the delta
function in n dimensions, then
) denotes the delta
function in n dimensions, then
 (n)(x
-
(n)(x
-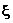 ) =
) =
 (x1-
(x1-
 1)
1)
 (x2-
(x2-
 2)...
2)...
 (xn-
(xn-
 n).
n).
 2
u + u = f(x),
(17.9)
2
u + u = f(x),
(17.9)
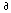 u/
u/
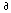 x1 = 0 when x1 = 0 or 1, and
x1 = 0 when x1 = 0 or 1, and
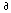 u/
u/
 x2 = 0 when x2 =
0 or 1.
x2 = 0 when x2 =
0 or 1.