Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod
(Some remarks for the instructor).
version of 16 September 2000.
Some of the calculations of this chapter are available in a Maple worksheet or in a Mathematica notebook.
Until now we have studied partial differential equations in one space dimension, x. Now we are ready to consider some problems in two or three space dimensions. Fortunately, the technique of separation of variables in more dimensions presents only a few new conceptual issues, and the technical complications are quite manageable.
In three space dimensions the wave equation has the form:
 u (some texts prefer
the notation
u (some texts prefer
the notation
 u).
It is sometimes convenient to think of
u).
It is sometimes convenient to think of
 u as the
Laplace operator
u as the
Laplace operator
 applied to u.
applied to u.
The heat equation in more than one space dimension likewise involves the Laplace operator:
 u.
u.
(9.1)
or, in three dimensions,
(9.2)
Laplace's equation arises in many other applications as well. It is the equation which describes the
Solutions of Laplace's equation are called harmonic functions.
Let's begin with the two-dimensional Laplace equation on a rectangle
Laplace's equation is the prototype of an elliptic equation, with different qualitative properties from either hyperbolic equations (like the wave equation) or parabolic equations (like the heat equation). The auxiliary conditions that are imposed are quite different from those for the wave equation. Specifically, we are normally given boundary conditions on the entire boundary, and are not specially concerned with an "initial" value of either variable x or y. Dirichlet boundary conditions for this problem are typically nonhomogeneous, of the form:
Separation of variables works much as it did for the heat equation and the wave equation. As with our earlier equations, we begin with the ansatz that u is a product solution
Rather than tackling four non-homogeneous boundary conditions (9.3)-(9.6) all at once, we begin by setting three of the four boundary functions to 0. For definiteness, we also make a specific choice of the fourth while developing the ideas:
Model Problem IX.1. Let us solve Laplace's equation with boundary conditions which are homogeneous on three of the four sides of a rectangle:
Separation begins much as before, but note that boundary condition (9.8) is not homogeneous, so it is not consistent with the superposition principle. If we add two functions satisfying (9.8), for example, we will get a function with the boundary value 2, not 1, when x = a. As in our earlier solutions by separating variables, let us guess that the solution is a product, u(x,y) = X(x) Y(y), and subsitute into Laplace's equation (9.1). Dividing through by X(x) Y(y), we find that
Evidently, if the y-independent quantity X''/X equals the x-independent quantity -Y''/Y, both must be a constant, and we have the familiar ordinary differential equations,
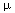 X
X
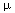 Y
Y
A good rule of thumb in this subject is to deal with the most homogeneous boundaries first. It is the variable y which has two homogeneous boundary conditions in this case, and it satisfies essentially the same eigenvalue problem as we have seen in previous chapters:
This same constant 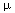 n
enters in to the X equation, but with the other sign. The general
solution for X is a linear combination of
exp(n
n
enters in to the X equation, but with the other sign. The general
solution for X is a linear combination of
exp(n x/2) and
exp(- n
x/2) and
exp(- n x/2),
rather than sines and cosines. There is a better choice for the
basis of this solution space, though, namely
x/2),
rather than sines and cosines. There is a better choice for the
basis of this solution space, though, namely
 x/2) + C2 sinh(n
x/2) + C2 sinh(n
 x/2).
x/2).
 x/2).
x/2).
This is a Fourier sine series in the variable y, with the complication that the coefficients have an extra factor,
 /2).
/2).
then the Fourier coefficients are easily calculated as:
 ) if n is odd, and otherwise 0.
) if n is odd, and otherwise 0.
 /2).
The solution becomes
/2).
The solution becomes
Let us rename the solution we just obtained for the simplified boundary conditions
Next, suppose that we had the boundary conditions :
Let us turn our attention now to a fully multidimensional problem. There will be few new concepts, though as we shall see the additional dimensions require some extra book-keeping with several indices to label the pieces of the solution correlating with the various dimensions. We illustrate the topic in a specific example.
Model Problem IX.2. How a mathematician cooks a cube steak. Consider
how to cook a steak which is one meter on a side (it is a
whale steak)
under the following conditions.
boundary conditions : The steak will be put into a preheated oven at temperature 200 C at time t=0.
IC: At time t=0, the steak is pulled directly from the freezer (u(0, x,y,z) = 0) and
put into the oven for four hours.
We wish to find the temperature throughout the interior of the steak at that time. Since the mathematician shops at a terrible meat market (but doesn't really notice), we may as well assume that the steak has the thermal properties of wood, so that in the heat equation, k = 2500 cm^2/hr.
Solution.
Instead of directly solving for the temperature, let u(t,x,y,z) be the temperature minus 200 C, in order to have homogeneous Dirichlet boundary conditions. With this change, for all t>0 the conditions on the six faces of the cube are
Step 1. Construct a general solution by separation of variables.
Suppose as usual that a solution of the heat equation is a product of the form
How do we solve this equation? Why, by separating variables again, of course! Let
Q(x) = X(x) Y(y) Z(z)
and evaluate
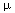 1 X
1 X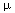 2 Y
2 Y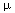 3 Z
3 Z
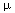 =
=
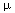 1 +
1 +
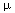 2 +
2 +
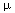 3,
3,
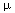 1 and X are of the form
1 and X are of the form
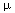 1 = (m1
1 = (m1
 /100)2, X(x) = sin(m1
/100)2, X(x) = sin(m1
 x /100), m1 = 1, 2, ....
x /100), m1 = 1, 2, ....
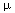 2 = (m2
2 = (m2
 /100)2,
Y(y) = sin(m2
/100)2,
Y(y) = sin(m2  y /100), m2 = 1, 2, ...,
y /100), m2 = 1, 2, ...,
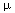 3 = (m3
3 = (m3
 /100)2, Z(z) = sin(m3
/100)2, Z(z) = sin(m3
 z /100), m3 = 1, 2, ....
z /100), m3 = 1, 2, ....
Step 2.
The constants will be determined by the initial conditions when we set t=0, obtaining a triple Fourier sine series. In this model problem the coefficients need to satisfy
You may find it more congenial, however, to rely on the usual, one-variable
Fourier sine series,
as follows. Imagine for the moment that y and z are fixed. What remains is a
function of x, and we could use the orthogonality of the functions sin(m1
 x/L)
to remove the sum over m1:
x/L)
to remove the sum over m1:
 x /100) and sin(n1
x /100) and sin(n1
 x /100) are orthogonal unless
m1=n1,
so only one term survives from the sum over m1.
x /100) are orthogonal unless
m1=n1,
so only one term survives from the sum over m1.
If we now multiply by sin(n2
 y/100) and integrate from 0 to 100, which
will eliminate all but one term in the sum over m2:
y/100) and integrate from 0 to 100, which
will eliminate all but one term in the sum over m2:
 z /100) and integrate over z:
z /100) and integrate over z:
 3.
3.
IX.1. Derive solutions (9.11)-(9.13) carefully.
IX.2. Find the solution of
Laplace's equation with mixed Dirichlet and Neumann
boundary conditions :
u(0,y) = f1(y)
u(a,y) = f2(y)
uy(x,0) = f3(x)
uy(x,b) = f4(x)
Hint: Solve four simpler problems, each of which has three of these functions equal to zero. Then sum the results.
IX.3. Find the solution of
Laplace's equationwith the more specific mixed Dirichlet and Neumann
boundary conditions :
u(0,y) = y
u(1,y) = 0
uy(x,0) = 0
uy(x,2) = 1
IX.4. Find the specific solution of Model Problem IX.2 by regarding the functions
sin(n1
 x /100) sin(n2
x /100) sin(n2
 y /100) sin(n3
y /100) sin(n3
 z /100)
z /100)
directly as an orthonormal set on the cube.
IX.5. Change the boundary conditions of Model Problem IX.2 so that two of the faces of the cube are insulated, i.e., Neumann Dirichlet 9.14) on all six faces (but at coordinates 0 and 1, not 0 and 100).
a) Find the normal modes of vibration.
b) Solve the initial-boundary value problem with initial conditions
u(0,x,y,z) = xyz sin(
 x)sin(
x)sin(
 y)sin(2
y)sin(2
 z)
z)
ut(0,x,y,z) = sin(2
 x).
x).