*(c) Copyright 2000 by Evans M. Harrell
II and James V. Herod. All rights reserved.
(Some remarks for the instructor).
version of 11 May 2000
The fundamental solution of the heat equation
In this chapter we return to the subject of the heat equation, first
encountered in
Chapter VIII. The
heat equation reads
 (20.1)
(20.1)
and was first derived by
Fourier
(see derivation). The same equation
describes the diffusion of a dye or other substance in a still fluid, and
at a microscopic level it results from random processes. We shall use
this physical insight to make a guess at the fundamental solution for the heat equation.
The term fundamental solution is the equivalent of the Green
function for a
parabolic PDE like the heat
equation (20.1). Since the equation is homogeneous, the
solution operator will not be an integral involving a forcing
function. Rather, the solution responds to the initial and boundary
conditions.
In order to limit the complications, we shall begin with the problem
of diffusion in one space dimension, and place the boundaries at
infinity, so the conditions will not be looked at explicitly. (Implicitly,
there is a condition of boundedness; if we allowed the addition of
uunbounded(t,x) = x, for example, the problem would
be in the
second Fredholm alternative.)
XX.1. A well-posed problem for the one-dimensional
heat equation would be of the form:
 (20.2)
(20.2)
for - < x <
< x <  and
0 < t <
and
0 < t <  , with given initial data:
, with given initial data:
u(0,x) = f(x).
The solution depends linearly on the initial data f(x), since (20.1)
is a homogeneous linear equation, so we can hope that the solution operator is an integral operator of the form
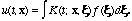 (20.3)
(20.3)
Definition XX.2. Suppose that A is a
linear operator on a
suitable space of functions of x, and that u satisfies
ut = A u, u(0,x) = f(x).
(20.4)
If there is a solution operator of the form (20.3), then
K(t; x, 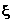 )
is referred to as
a fundamental solution of (20.4).
)
is referred to as
a fundamental solution of (20.4).
Au usual for
Green functions, there is an
intuitive physical meaning to the fundamental solution: It is the
solution with initial data
u(0,x) = 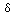 (x-
(x-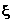 ).
Once we have this solution, any solution with other initial data can be
thought of as a continuous superposition of solutions with these
simpler, but singular, initial conditions.
).
Once we have this solution, any solution with other initial data can be
thought of as a continuous superposition of solutions with these
simpler, but singular, initial conditions.
There are several ways to derive the fundamental solution of
the
heat equation in unrestricted space. For example,
we could apply either the
Fourier
or
Laplace
transforms, in the spatial variables x, to obtain a differential
equation involving only t, and then transform back. Instead,
here we use the physics of diffusion as a hint to form an
ansatz for the solution and then
make a calculation.
We take the opportunity at this stage to scale
time to make the constant in the
heat equation
k=1;
the mathematically natural time variable is t' = kt.)
The hint is that the underlying mechanism is some sort of
random process which is isotropic, unrestricted in space, and
invariant in time, then we might expect that the density u(t,x) could
be a Gaussian distribution, and once it has this distribution, it
should remain a Gaussian, although it will spread out as time goes by.
A Gaussian density on the x-axis, centered at x=0,
is of the form
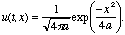 (20.5)
The normalization is taken so that the integral of the
Gaussian density is 1. If we are right, we should be
able to find a function a(t) so that
the function (20.5) solves the
one-dimensional heat equation. Let's plug
in and see what we get:
(20.5)
The normalization is taken so that the integral of the
Gaussian density is 1. If we are right, we should be
able to find a function a(t) so that
the function (20.5) solves the
one-dimensional heat equation. Let's plug
in and see what we get:
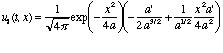 whereas a slightly longer calculation reveals that
whereas a slightly longer calculation reveals that
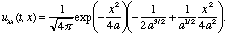
These differ only by the factor a'(t). Gratifyingly, the ansatz works
with the very simple choice a(t) = t. We now take a closer look at the
fundamental solution we have found:
Definition XX.3. The function
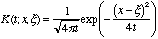 is known as the one-dimensional heat kernel.
is known as the one-dimensional heat kernel.
(See the
exercises for some alternative ways to derive the
heat kernel.)
We have not yet explained in what sense the heat kernel approaches
the delta function as t tends to 0. Notice that the Gaussian
distribution of the
heat kernel
becomes very narrow when t is small, while the
height scales so that the integral of the distribution remains one.
Hence if we integrate it by any continuous, bounded
function f(pix/bfxi.gif)
and take the limit, we will in fact get f(x).
In the contrary limit, the distribution becomes very broad,
corresponding to our experience that a diffusing substance tends to
a widespread, nearly uniform, density.
Model Problem XX.4. Suppose k=1 in
(20.2) and the initial condition is
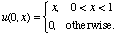 Solve for u(t,x).
Solve for u(t,x).
Solution. We perform the integral
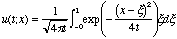 with software, and find
with software, and find
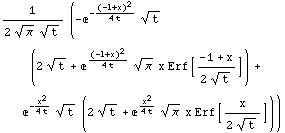 Here Erf denotes the error function of statistics,
Here Erf denotes the error function of statistics,
![Erf[z] := 2 pi^(-1/2) int(exp(-s^2) ds, s=0..z)](pix/ch20p10.GIF)
An additional convenient feature of the heat kernel is that
the extension to many dimensions is immediate, as can be verified
by directly plugging into the
heat equation:
Definition XX.5. The function
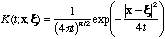 is the heat kernel for Rn.
is the heat kernel for Rn.
In addition to helping us solve problems like
Model Problem XX.4, the
solution of the
heat equation with the heat kernel
reveals many things about what the solutions can
be like. For example, if f(x) is any bounded function,
even one with awful discontinuities, we can differentiate
the expression in (20.3) under the
integral sign. In fact, we can differentiate as often as we like.
This means that an initially irregular distribution of temperature
or a diffusing substance, is instantaneously smoothed out.
Perhaps this is not too surprising when we think that the heat
kernel itself solves the heat equation, and changes instantaneously
from a delta function to a smooth, Gaussian distribution.
Model Problem XX.6. Again consider the
one-dimensionalheat equation with k=1, but
include a source of heat which is constant in time:
ut - uxx = f(x),
(20.6)
u(0,x) = g(x)
for two given functions f(x) and g(x) defined for
-
 < x <
< x <

Solution. Let's try to reduce this problem to the familiar
(20.1) solved
by the fundamental solution we already
know, by subtracting something off to make (20.6) homogeneous.
One way to do this is to write
w(t,x) = u(t,x) + F(x), where F''(x) = f(x). That is, F(x) is any second
integral of f(x). By substituting, we find that
wt - wxx = ut - uxx - f(x) = 0,
w(0,x) = g(x) + F(x).
Hence the solution is
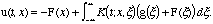
Exercises XX
-
Solve the initial-value problem for -
 < x <
< x <
 :
ut = uxx,
:
ut = uxx,
u(0,x) = exp(-|x|)
-
Use the
free heat kernel and the
method of images of
Chapter XIX to find the fundamental
solution for the initial-boundary-value problem for
0 < x <
 :
ut = uxx,
:
ut = uxx,
u(t,0) = 0
u(0,x) = g(x) (a given function)
-
Use the
free heat kernel and the
method of images of
Chapter XIX to find the fundamental
solution for the initial-boundary-value problem for
0 < x <
 :
ut = uxx,
:
ut = uxx,
ux(t,0) = 0
u(0,x) = g(x) (a given function)
-
Use the
free heat kernel and the
method of images of
Chapter XIX to find the fundamental
solution for the initial-boundary-value problem for
0 < x < 1:
ut = uxx,
u(t,0) = u(t,1) = 0
u(0,x) = g(x) (a given function)
Compare the infinite-series you obtain with the solution using
separation fo variables from
Chapter VIII.
-
Solve
(20.6) with g(x) = 0, but f(x) = 1 for
-1 < x < 1, and 0 otherwise.
-
Extend the solution to
Model Problem XX.6 to the case where
ut - uxx = f(x) + h(t),
u(0,x) = g(x)
for three given functions f(x), g(x), and h(t).
-
Solve the three-space-dimensional initial-value problem:

u(0,x) = 1 for |x| < 1 and 0 otherwise.
Verify that the solution is continuous for all t > 0.
-
Make a change of variables for the
heat equation of the following form:
r := x/t1/2,
w := u(t,x)/u(0,x).
Show that if we assume that w depends only on r, the heat equation
becomes an ordinary differential equation, and
the heat kernel is a solution.
- (For students who are familiar with the
Fourier transform.)
Derive the heat-kernel by use of the
Fourier transform in the x-variable. (Hints: This will produce an ordinary differential equation in the variable t, and the inverse Fourier transform will produce the heat
kernel. It may also help to notice that the Fourier transform of
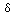 (x-
(x-
 ) is
) is
(2  )-1/2
exp(i k
)-1/2
exp(i k
 ).
).
-
Consider the two-dimensional heat equation
ut =
 2 u,
on the half-space where y > x.
2 u,
on the half-space where y > x.
(a) Find the fundamental solution for this PDE with zero Dirichlet boundary
conditions, i.e.,
u(t;x,x) = 0.
(b)
Solve the initial-boundary value problem with
u(0;x,y) = 2.
Link to
Chapter XXI
chapter XIX
Table of Contents
Evans Harrell's home page
Jim Herod's home page
 < x <
< x < 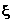 )
is referred to as
a fundamental solution of (20.4).
)
is referred to as
a fundamental solution of (20.4).
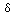 (x-
(x- ) is
) is
 )-1/2
exp(i k
)-1/2
exp(i k
 2 u,
2 u,