 2u = f on D,
2u = f on D,
u = g on the boundary of D.
Linear Methods of Applied Mathematics
Evans M. Harrell II
and
James V. Herod*
In this section we shall construct Green functions for the problems of the type: Find u such that
 2u = f on D,
2u = f on D,
(19.1)
This partial differential equation is known as
Poisson's equation, and its solutions
may be thought of as the electrostatic potential in the presence of a
charge distribution
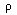 , related to f by
, related to f by

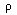 .
.
For physical reasons we expect that knowing the charge in the interior and the potential on the boundary of a region is sufficient to determine the potential in the interior uniquely. Indeed, a uniqueness theorem guarantees precisely the problem is well posed in this sense.
In order to simplify notation, we will let P or Q represent points in the plane. For example, P might represent {x,y} and Q represent {a,b}. We indicate that in two dimensions,
 2G(P,
Q) = Gxx + Gyy,
2G(P,
Q) = Gxx + Gyy,
 p2G(P,Q).
p2G(P,Q).
The function G is to be constructed to have these properties:
 p p2 G(P,Q) =
p p2 G(P,Q) =
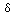 (P,Q)
(P,Q)
(19.2)
Thus, having such a G and knowing f and g, we have a formula for u which provides a solution to the problem:
How is such a G constructed? We will do it in two pieces. We construct G = F + R where F is the free Green function (also known as the fundamental or singular part) and satisfies:
 2 G =
2 G =
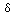
 (in polar coordinates).
(in polar coordinates).
(19.3)
R is the regular part and satisfies
(19.4)
Let us recall that whenever we have a linear, inhomogeneous problem, the general solution is given by any particular solution, plus the general solution of the related homogeneous problem. Equation (19.4) is the homogeneous equation associated with (19.3). It has no delta function, so its solutions will be completely regular. (Even if the boundary conditions were rough this is guaranteed by a general theorem for Laplace's equation.)
In other words, the singular parts of any two Green functions for the same equation, but different boundary conditions, will be the same. So let us find that singular part in the simplest possible situation, which is (19.3).
We begin by constructing F. Recall the formula for
the Laplace operator
 2 in polar
coordinates:
2 in polar
coordinates:
(19.5)
In seeking F such that
,
we recall that, in the sense of
distributions,
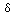 ({x,y},{a,b}) = 0 unless {x,y} = {a,b}. Also,
({x,y},{a,b}) = 0 unless {x,y} = {a,b}. Also,
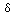 is radially
symmetric. Thus, supposing initially that
Q = {a,b} is at the origin, we have
is radially
symmetric. Thus, supposing initially that
Q = {a,b} is at the origin, we have
This last equality is because F is independent of
 . Thus
r Fr is constant and F(r) = A ln(r) + B for
some A and B. It remains to find A and B. To this point we have not used
information about F at the origin, only at {x,y} different from {0,0}.
Information about F at {a,b} comes through the integral. If we integrate the
delta function over any disk with radius c > 0 we get 1, so:
. Thus
r Fr is constant and F(r) = A ln(r) + B for
some A and B. It remains to find A and B. To this point we have not used
information about F at the origin, only at {x,y} different from {0,0}.
Information about F at {a,b} comes through the integral. If we integrate the
delta function over any disk with radius c > 0 we get 1, so:
Thus, A = 1/(2
 ) and B is undetermined. We may as well choose it to be 0
at this stage. Of course there is no singularity in the constant function, so
its derivatives do not contribute to the delta function. When
Q is not at the
origin, we simply shift the calculation by
Q:
) and B is undetermined. We may as well choose it to be 0
at this stage. Of course there is no singularity in the constant function, so
its derivatives do not contribute to the delta function. When
Q is not at the
origin, we simply shift the calculation by
Q:
 ).
).
 )
)
The function F is the Green function for the following problem:
This problem is in the first alternative, as a consequence of a theorem of Liouville for solutions of Laplace's equation (known as harmonic functions ), which implies that the only square-integrable solution is 0. See exercise 3 for why the assumption that u is square integrable is necessary. Some mild assumptions on f are needed, for instance |f| could be assumed bounded by any large constant times (1 + r)-3.
We next discuss a method for finding the Green function on regions other than Rn. This method may apply if the region is highly symmetric:
Model Problem XIX.1. Now let us solve the problem (19.1) on a new domain, the upper half plane, where x may have any value but y > 0. We need to find a Green function which = 0 when y = 0.
Solution. We may as well imagine that the problem we wish to solve is (19.1) for y > 0, with the boundary condition
u(x,0) = 0,
for it has the same Green function as other with more complicated Dirichlet boundary data on the x-axis, as shown above.
Here are two ways to derive the Green function.
I. The problem (19.1) is well-posed problem, owing to the uniqueness theorem. Thus if we can find a solution by imagining a different situation which is easier to solve, but which satisfies the partial differential equation and the boundary condition, it must be the right solution. The different situation will be one on all of R2, like the problem we just solved, but where the boundary condition happens to be satisfied. Here is how:
Since f(x,y) is physically meaningful only for y > 0, we are free to define it however we will when y < 0. Let us choose to define it by the odd extension , so f(x,-y) = - f(x,y). We can solve this modified problem with the free Green function, as
(19.6)
The last step here came from rewriting the integral over y < 0 using the odd symmetry. Notice that if y=0, this integral vanishes, while for y > 0, the extended function f has the same values as posited in the problem. Because of uniqueness, it is the right solution to the problem on the upper half plane. The Green function for the half-plane problem is
(19.7)
where PR = {x,-y} is the point found by reflecting P across the x-axis. It is as if there were an equal and opposite image source for the problem, located in the lower half plane.
II. Here is another way to derive the solution (19.6) and the Green function (19.7). As remarked above, the Green function for this problem is of the form
 2 F(S,Q) = 0
2 F(S,Q) = 0
Let's use the method of images to solve some more problems. First, we would like to note that the idea of exploiting symmetries together with the uniqueness theorem is not logically connected to the method of Green functions, but can be used in conjunction with any method of solution. Indeed, we used the same ideas in our discussion of d'Alembert's solution of the wave equation.
Model Problem XIX.2. We continue here to solve Poisson's equation (19.1), but now on the strip D = {x unrestricted, 0 < y < 1}. Dirichlet boundary conditions are imposed on the strip.
Solution. Have you ever been in a barber shop or hair dresser where you sit
between two mirrors? You see an infinite number of reflections of yourself,
alternating as to whether they face toward you or away from you. If we want to
place image Green functions in the plane to match both boundary conditions, we
need an infinite number of them. The position reflected from height y<1
through y=1 is 2 - y (when y=0 the reflection is at 2 and when y=1 it meets
its reflection). The next reflection will be at 2+y, the next one at 4 - y,
and so forth. We need to alternate signs to get all the cancellations. The
result ought to be:
infinity - infinity.
Remember, however, that we can subtract a regular solution of
Laplace's
equation
(It should be easy to see that c (y-b) solves Laplace's equation for any
b,c.)
Model Problem XIX.3. We continue to solve
Poisson's equation
(19.1),
again on the upper half-plane y>0, but this time with Neumann-type boundary
conditions,
In some ways things are simpler in three dimensions for this problem. Let us
now seek the three-dimensional free Green function with the same technique as we
used above. We begin by looking for a solution of Laplace's equation which
depends only on the radial coordinate in the spherical coordinate system. In
this system, the Laplace operator has the form
Again, we may choose B = 0 in most circumstances, and use the divergence
theorem to evaluate A:
For those of you who have an interest in electromagnetism, this may be familiar
as the electric potential of a unit charge (with a certain choice of physical
units and a sign convention which may be the opposite of what you will find in
a physics class). If there is a continuous charge distribution
The method of images works in three dimensions just as in two dimensions:
Model Problem XIX.4. Now let us solve
Poisson's equation on the
upper half space, where x and y may have any value but z > 0. We
need to find a Green function which = 0 when z = 0.
Solution: If
P = {a,b,c} and Q = {x,y,z}, then the Green function is:
In order to determine this region, let us choose the x-axis so that
Armed with this knowledge, it is a matter of algebra to go the other way and
find the values of
Q' and q which produce the correct Green function for any
particular sphere. Supposing that the sphere is centered at the origin and has
radius R. If
Q = (a1,0,0) we find:
q = -R/a1.
If Q is not located on the x-axis, we can find q and
Q' simply by rotating this
relationship: Q' = Q R2/|Q|2, and q
= R/|Q|.
Theorem XIX.5. The Green function for Poisson's equation in the sphere of
radius R (or, in two-dimensions, the circle of radius R), with Dirichlet
boundary conditions, is
Gy({x,y},
Q) = 0 when y = 0.
where r is the radial coordinate, on the full three-dimensional space
R3.
where f(x) = 1 for |x| < 2 and 0 otherwise, on the domain x < 4, y
and z unrestricted. Impose the boundary condition.
(The solutions of this equation are known as modified Bessel functions.)
(19.8)
and to sum the images in the following way:
(19.9)
(19.10)
 |P - Q|).
|P - Q|).
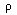 (P),
then the electrostatic potential in free space is the solution of
(P),
then the electrostatic potential in free space is the solution of
 2u =
- 4
2u =
- 4 
There is another remarkable situation in which the method of images is useful.
For motivation, suppose we work the problem in reverse, but trying to locate a
new region on which we can solve
(19.2) with zero Dirichlet boundary conditions.
For example, if we look at
(19.11)
Exercises XIX
v = (x2+y2)1/2 - x,
b) x + 3 y
c) x y + 1
d) x2 - y2
e) cos(x) sinh(y)
ux(0,y) = 0.
 n) - ln(2) /(2
n) - ln(2) /(2
 ) - ln(n)/(2
) - ln(n)/(2
 ).
).
-
 u = f(x)
u = f(x)
where k is a nonzero constant. u - k2 u
= f(x)
u - k2 u
= f(x)
Link to