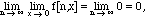
Linear Methods of Applied Mathematics

Evans M. Harrell II and James V. Herod*

*(c) Copyright 1994-1997 by Evans M. Harrell II and James V. Herod. All rights reserved.

version of 3 November 1997,

If you wish to print a nicely formatted version of this chapter, you may download the rtf file, which will be interpreted and opened by Microsoft Word or the pdf file, which will be interpreted and opened by Adobe Acrobat Reader.

Many of the calculations in this chapter are available in the format of a Mathematica notebook or Maple worksheet.

(Some remarks for the instructor).

V. Differentiating Fourier Series

One of the most important uses of Fourier series is as a tool in solving differential equations. Because of that we will frequently want to differentiate a Fourier series. Since the Fourier series, like any infinite series, is a limit, questions can arise about whether it is permissible to differentiate in x before summing in n. In your advanced calculus class you should have seen examples where interchanging the order of two limits leads to different answers. This can happen quite easily.

Example V.1. Let f[n,x] := 0 if -1/n <= x <= 1/n, and 1 otherwise - i.e. the indicator function (as in chapter III) of the complement of the interval [-1/n, 1/n]. Then f[n,0] = 0 for all n, so if we let x tend to zero before n tends to infinity,

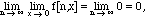
whereas if n tends to infinity first,

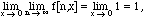
One of the great things about Fourier series is that, despite a very reasonable worry, it is usually completely reliable to interchange limits. Indeed, one nice way to calculate Fourier series is to differentiate or integrate other Fourier series. We'll do some examples and see how reliable the answer is, as well as a couple of situations where we have to be careful. As usual, there is a Mathematica notebook paralleling the text of this chapter

With the formulae for the Fourier coefficients given in Chapter II it is a routine matter to calculate the Fourier series for the function x - x³ defined for -1 < x < 1. We find that there are no cosine contributions, and

To get a feel for this series, let us plot the sum of the first three terms and compare with x-x³:

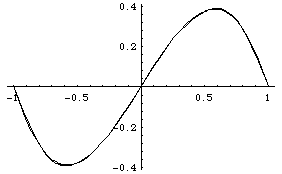
Wonderful! The function and the truncated series match rather closely.

What happens if we differentiate?

Model Problem V.1. Differentiate the terms in the Fourier series for this function, and compare with 1 - 3 x².

Solution.

If we differentiate the series for x-x³, we get the series

supposing that it is legitimate to differentiate the infinite series term by term. (Sometimes it definitely is not.) We could calculate the Fourier series for 1-3x² directly with the formulae of chapter IV, either by hand or with software as in the Mathematica notebook or the Maple worksheet, and compare, but before doing so, let's evaluate the differentiated series on its own merits. First note that the function 1-3x² is even, so there will only be cosine contributions, as we have found. Next, let us plot the sum of the first four terms in the differentiated series and compare with the exact function:

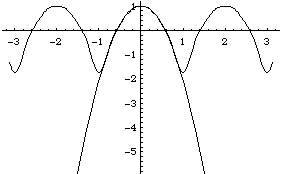
Remember - the Fourier series always corresponds to the periodic extension of the function on the basic interval. The formula 1 - 3x² is not valid for the series outside [-1,1].

Finally, let us calculate the Fourier series using the integral formulae from Chapter II. The result, for example using the Mathematica notebook or the Maple worksheet, is

    a₀ = 0,
    a_k = 12 (-1)^k+1/(k) ², k = 1, 2, ...,

as expected. (Notice that this example has something to do with the Legendre polynomials.)

Suppose now that instead of differentiating, we integrate a Fourier series term by term. If a₀ (which = c)₀ is different from 0, we get another Fourier series! If a₀ is not 0, then we would only get another Fourier series after replacing the function x with a Fourier series, but we won't consider that case now.

Does the integrated series converge to the integral of the original function? According to our experiment with differentiation, it seems so. Let us try again, by integrating the series for x - x³term by term. We find:

What does this show about the constant of integration? When we integrated the series we got the integral with average average a₀, chosen here as 0. Remember that a₀ is always the average of the function. The difference in height between the two graphs is just the average of x²/2 - x⁴/4, which doesn't happen to be 0.

Exercise V.1. Use the tricks of this chapter to calculate the Fourier series for the functions xⁿ, n = 0, 1, ..., on the interval -1 < x < 1.

Exercise V.2. What series do you obtain by differentiating the Fourier series for the square pulse (cf. Model Problem IV.1)? If you know about the "Dirac" delta function, comment on the relationship between the series you get for the square pulse and the one for the delta function delta(x-a) (periodically extended).

          (solution by Mathematica)

Exercise V.3. Consider what happens when a Legendre series is differentiated term by term. Is the result a Legendre series? Does the result converge to the derivative of the original function?

Exercise V.4. Check the convergence of Exercise V.3 numerically in a specific example such as f(x) = sin(¼x), -1 < x < 1.

Onward to chapter VI (red syllabus)

Onward to chapter XII (yellow syllabus)

Back to chapter IV

Return to Table of Contents

Return to Evans Harrell's home page